浙江省绍兴市2019年中考数学预测卷1
试卷更新日期:2019-04-29 类型:中考模拟
一、选择题(本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
-
1. 5的相反数是( )A、5 B、 C、 D、﹣52. 12的负的平方根介于( )A、﹣5与﹣4之间 B、﹣4与﹣3之间 C、﹣3与﹣2之间 D、﹣2与﹣1之间3. 在下列几何体中,三视图都是圆的为( )A、
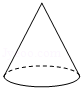 B、
B、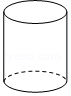 C、
C、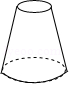 D、
D、 4. 从标有1,2,3,4的四张卡片中任取两张,卡片上的数字之和为奇数的概率是( )A、 B、 C、 D、5. 下列计算的结果是x5的为( )A、x10÷x2 B、x6﹣x C、x2•x3 D、(x2)36. 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系.下列说法中错误的是( )
4. 从标有1,2,3,4的四张卡片中任取两张,卡片上的数字之和为奇数的概率是( )A、 B、 C、 D、5. 下列计算的结果是x5的为( )A、x10÷x2 B、x6﹣x C、x2•x3 D、(x2)36. 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系.下列说法中错误的是( )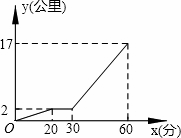 A、小强从家到公共汽车站步行了2公里 B、小强在公共汽车站等小明用了10分钟 C、公共汽车的平均速度是30公里/小时 D、小强乘公共汽车用了20分钟7. 把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大 ;若边长扩大5倍,则面积扩大 。( )A、5倍,10倍 B、10倍,25倍 C、 倍,25倍 D、25倍,25倍8. 如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m,n的关系是( )
A、小强从家到公共汽车站步行了2公里 B、小强在公共汽车站等小明用了10分钟 C、公共汽车的平均速度是30公里/小时 D、小强乘公共汽车用了20分钟7. 把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大 ;若边长扩大5倍,则面积扩大 。( )A、5倍,10倍 B、10倍,25倍 C、 倍,25倍 D、25倍,25倍8. 如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m,n的关系是( )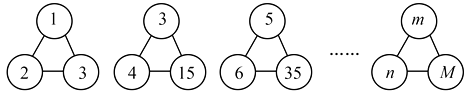 A、M=mn B、M=n(m+1) C、M=mn+1 D、M=m(n+1)9. 已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数y=﹣ x2+2x+5 图象的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )
A、M=mn B、M=n(m+1) C、M=mn+1 D、M=m(n+1)9. 已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数y=﹣ x2+2x+5 图象的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )
A、0米到8米 B、5米到8米 C、 到8米 D、5米到 米10. 在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为( )A、 B、 C、 或 D、 或二、填空题(本大题共6小题,每小题5分,共30分)
-
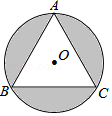
11. 若x2y+xy2=30,xy=6,则x2+y2= , x﹣y= .12. 如图,△ABC是半径为2的圆内接正三角形,则图中阴影部分的面积是(结果用含π的式子表示).
 13. 如图,在△ABC中, ,DE是AB的垂直平分线,∠BAD:∠CAB=1:3,则∠B= .
13. 如图,在△ABC中, ,DE是AB的垂直平分线,∠BAD:∠CAB=1:3,则∠B= .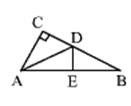 14. 如图,A.B是反比例函数y= 图象上关于原点O对称的两点,BC⊥x轴,垂足为C,连线AC过点D(0,﹣1.5).若△ABC的面积为7,则点B的坐标为 .
14. 如图,A.B是反比例函数y= 图象上关于原点O对称的两点,BC⊥x轴,垂足为C,连线AC过点D(0,﹣1.5).若△ABC的面积为7,则点B的坐标为 .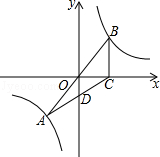 15. 如图①,在四边形ABCD中,AD∥BC,∠C=90°,CD=6cm.动点Q从点B出发,以1cm/S的速度沿BC运动到点C停止,同时,动点P也从B点出发,沿折线B→A→D运动到点D停止,且PQ⊥BC.设运动时间为t(s),点P运动的路程为y(cm),在直角坐标系中画出y关于t的函数图象为折线段OE和EF(如图②).已知点M(4,5)在线段OE上,则图①中AB的长是 cm.
15. 如图①,在四边形ABCD中,AD∥BC,∠C=90°,CD=6cm.动点Q从点B出发,以1cm/S的速度沿BC运动到点C停止,同时,动点P也从B点出发,沿折线B→A→D运动到点D停止,且PQ⊥BC.设运动时间为t(s),点P运动的路程为y(cm),在直角坐标系中画出y关于t的函数图象为折线段OE和EF(如图②).已知点M(4,5)在线段OE上,则图①中AB的长是 cm.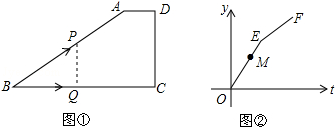
三、解答题(本大题共8小题,共80分)
-
16.
(1)、计算:|2﹣ |+( +1)0﹣3tan30°+(﹣1)2018﹣( )﹣1;(2)、解不等式组: 并判断﹣1, 这两个数是否为该不等式组的解.17. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表: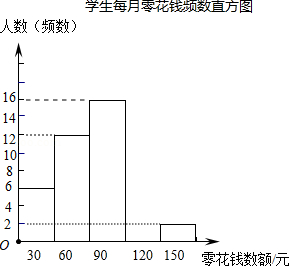
请根据以上图表,解答下列问题:
零花钱数额x/元
人数(频数)
频率
0≤x<30
6
0.15
30≤x<60
12
0.30
60≤x<90
16
0.40
90≤x<120
b
0.10
120≤x<150
2
a
(1)、这次被调查的人数共有人,a= .(2)、计算并补全频数分布直方图;(3)、请估计该校1500名学生中每月零花钱数额低于90元的人数.18. 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2). (1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.19. 某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:
(1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.19. 某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:销售第x天
第1天
第2天
第3天
第4天
…
第30天
销售单价m(元/件)
49
48
47
46
…
20
日销售量n(件)
45
50
55
60
…
190
(1)、观察表中数据,分别直接写出m与x,n与x的函数关系式: , ;(2)、求商场销售该商品第几天时该商品的日销售额恰好为3600元?(3)、销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?20. 如图,四边形ABCD、BEFG均为正方形,连接AG、CE.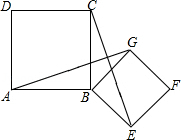 (1)、求证:AG=CE;(2)、求证:AG⊥CE.21. 如图所示,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD.
(1)、求证:AG=CE;(2)、求证:AG⊥CE.21. 如图所示,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD.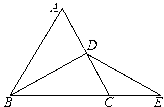 (1)、用尺规作图的方法,过D点作DM⊥BE,垂足是M;(不写作法,保留作图痕迹)(2)、求证:BM=EM.22. 定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)、用尺规作图的方法,过D点作DM⊥BE,垂足是M;(不写作法,保留作图痕迹)(2)、求证:BM=EM.22. 定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点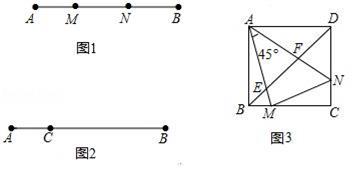 (1)、已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;(2)、已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可)(3)、如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F
(1)、已知点M,N是线段AB的勾股分割点,若AM=3,MN=4求BN的长;(2)、已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可)(3)、如图3,正方形ABCD中,M,N分别在BC,DC上,且BM≠DN,∠MAN=45°,AM,AN分别交BD于E,F求证:①E、F是线段BD的勾股分割点;
②△AMN的面积是△AEF面积的两倍.
23. 在平面直角坐标系中,直线y=﹣ x+1交y轴于点B,交x轴于点A,抛物线y=﹣ x2+bx+c经过点B,与直线y=﹣ +1交于点C(4,﹣2).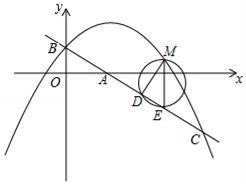 (1)、求抛物线的解析式;(2)、如图,横坐标为m的点M在直线BC上方的抛物线上,过点M作ME∥y轴交直线BC于点E,以ME为直径的圆交直线BC于另一点D,当点E在x轴上时,求△DEM的周长.(3)、将△AOB绕坐标平面内的某一点按顺时针方向旋转90°,得到△A1O1B1 , 点A,O,B的对应点分别是点A1 , O1 , B1 , 若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的坐标.
(1)、求抛物线的解析式;(2)、如图,横坐标为m的点M在直线BC上方的抛物线上,过点M作ME∥y轴交直线BC于点E,以ME为直径的圆交直线BC于另一点D,当点E在x轴上时,求△DEM的周长.(3)、将△AOB绕坐标平面内的某一点按顺时针方向旋转90°,得到△A1O1B1 , 点A,O,B的对应点分别是点A1 , O1 , B1 , 若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的坐标.