浙江省衢州市2019年中考数学预测卷

试卷更新日期：2019-04-29 类型：中考模拟

进入出卷网下载

一、选择题（共10小题）

1. 2018的相反数是（）

A、8102 B、﹣2018 C、 $\frac{1}{2018}$ D、2018

查看试题解析
2. 如图，直线AD，BC被直线BF和AC所截，则∠1的同位角和∠5的内错角分别是（）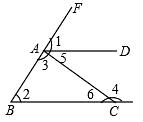

A、∠4，∠2 B、∠2，∠6 C、∠5，∠4 D、∠2，∠4

查看试题解析
3. 十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从54万亿元增长80万亿元，稳居世界第二，其中80万亿用科学记数法表示为（）

A、8×10¹² B、8×10¹³ C、8×10¹⁴ D、0.8×10¹³

查看试题解析
4. 下列几何体是由4个相同的小正方体搭成的，其中左视图与俯视图相同的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，点A，B，C是⊙O上的三点，若∠BOC＝50°，则∠A的度数是（）

A、25° B、20° C、80° D、100°

查看试题解析
6. 如图，任意转动正六边形转盘一次，当转盘停止转动时，指针指向大于3的数的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
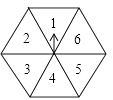7. 关于x的一元一次不等式 $\frac{1 - x}{3}$ +2≤ $\frac{x + 1}{2}$ 的解为（）

A、x≤ $\frac{1}{5}$ B、x≥ $\frac{1}{5}$ C、x≤ $\frac{11}{5}$ D、x≥ $\frac{11}{5}$

查看试题解析
8. 如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（）

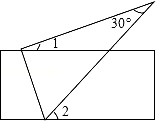A、30° B、40° C、50° D、60°

查看试题解析
9. 已知圆锥的底面半径为5cm，侧面积为60πcm² ，设圆锥的母线与高的夹角为θ，则sinθ的值为（）

A、 $\frac{3}{13}$ B、 $\frac{5}{13}$ C、 $\frac{5}{12}$ D、 $\frac{12}{13}$

查看试题解析
10. 如图，在⊙O中，直径AB与弦MN相交于点P，∠NPB＝45°，若AP＝2，BP＝6，则MN的长为（）

A、 $\sqrt{14}$ B、2 $\sqrt{5}$ C、2 $\sqrt{14}$ D、8

查看试题解析

二、填空题（共6小题）

11. 因式分解：m²﹣4n²= ．

查看试题解析
12. 李老师最近6个月的手机话费（单位：元）分别为：27，36，54，29，38，42，这组数据的中位数是．

查看试题解析
13. 如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得△ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是．

查看试题解析
14. 某日上午，甲，乙两车先后从A地出发沿同一条公路匀速前往B地，甲车8点出发，如图是其行驶路程s（千米）随行驶时间t（小时）变化的图象．乙车9点出发，若要在10点至11点之间（含10点和11点）追上甲车，则乙车的速度v（单位：千米/小时）的范围是．

查看试题解析
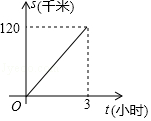15. 如图，A，B是反比例函数y＝ $\frac{4}{x}$ 在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和4，则△OAB的面积是．

查看试题解析
16. 在平面直角坐标系中，规定把一个点先绕原点逆时针旋转45°，再作出它关于原点的对称点称为一次变换，已知点A的坐标为（﹣2，0），把点A经过连续2014次这样的变换得到的点A₂₀₁₄的坐标是．

查看试题解析

三、解答题（共8小题）

17. 计算： $\sqrt{9} + \sqrt[3]{- 8} + {(π - 3)}^{0} - | - 2 | + {(- 1)}^{2}$ ．

查看试题解析
18. 已知，如图，平行四边形ABCD中，E是BC边的中点，连DE并延长交AB的延长线于点F，求证：AB＝BF．

查看试题解析
19. 还记得完全平方公式（a+b）²＝a²＝2ab+b²吗？当a，b＞0时，完全平方公式可以用图（1）来说明．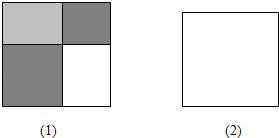

(1)、对图（2）进行适当的分割，猜想出（a+b+c）²的展开形式，并给出其推导过程；

(2)、通过求解本题，你有哪些收获？

查看试题解析
20. 超速行驶是一种十分危险的违法驾驶行为，在一条笔直的高速公路MN上，小型车限速为每小时120千米，设置在公路旁的超速监测点C，现测得一辆小型车在监测点C的南偏西30°方向的A处，7秒后，测得其在监测点C的南偏东45°方向的B处，已知BC＝200米，B在A的北偏东75°方向，请问：这辆车超速了吗？通过计算说明理由．（参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
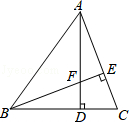
21. 某中学为了了解本校学生对球类运动的爱好情况，采用抽样的方法，从乒乓球、羽毛球、篮球和排球四个方面抽查了若干名学生，在还没有绘制成功的“折线统计图”与“扇形统计图”中，请你根据已提供的部分信息解答下列问题．

(1)、在这次调查活动中，一共调查了名学生；

(2)、通过计算，“排球”所在扇形的圆心角是多少度？

(3)、请补全折线统计图；

(4)、若该校有学生1300名，估计爱好篮球活动的约有多少名学生？

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，D为斜边AB上的中点，连接CD，以CD为直径作⊙O，分别与AC、BC交于点M、N．过点N作NE⊥AB，垂足为点E．

(1)、求证：NE为⊙O的切线；

(2)、连接MD，若NE＝3，sin∠BCD＝ $\frac{3}{5}$ ，求MD的长．

查看试题解析
23. 小明大学毕业回家乡创业，第一期培植盆景与花卉各50盆．售后统计，盆景的平均每盆利润是160元，花卉的平均每盆利润是19元．调研发现：
①盆景每增加1盆，盆景的平均每盆利润减少2元；每减少1盆，盆景的平均每盆利润增加2元；

②花卉的平均每盆利润始终不变．

小明计划第二期培植盆景与花卉共100盆，设培植的盆景比第一期增加x盆，第二期盆景与花卉售完后的利润分别为W₁ ， W₂（单位：元）．

(1)、用含x的代数式分别表示W₁ ， W₂；

(2)、当x取何值时，第二期培植的盆景与花卉售完后获得的总利润W最大，最大总利润是多少？

查看试题解析
24. 在平面直角坐标系xOy中，直线l₁：y＝k₁x+2 $\sqrt{3}$ 与x轴、y轴分别交于点A、B两点，OA＝ $\sqrt{3}$ OB，直线l₂：y＝k₂x+b经过点C（1，﹣ $\sqrt{3}$ ），与x轴、y轴和线段AB分别交于点E、F、D三点．

(1)、求直线l₁的解析式；

(2)、如图①：若EC＝ED，求点D的坐标和△BFD的面积；

(3)、如图②：在坐标轴上是否存在点P，使△PCD是以CD为底边的等腰直角三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析