浙江省宁波市2019年中考数学预测卷
试卷更新日期:2019-04-29 类型:中考模拟
一、选择题(每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列各式,错误的是( )A、-1<3 B、0>-5 C、-3>-2 D、-9<-82. 在今年的十一黄金周期间,新昌十九峰景区共接待海内外游客约11.2万人次,则数据11.2万用科学记数法可表示为( )A、11.2×104 B、11.2×105 C、1.12×104 D、1.12 ×1053. 下列各式中计算正确的是( )A、(x+y)2=x2+y2 B、(3x)2=6x2 C、(x3)2=x6 D、a2+a2=a44. 桌面上有A,B两球及5个指定的点,若将B球分别射向这5个点,则B球一次反弹后击中A球的概率为( )
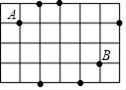 A、 B、 C、 D、5. 已知一多边形的每一个内角都等于150°,则这个多边形是( )A、十二边形 B、十边形 C、八边形 D、六边形6. 如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )
A、 B、 C、 D、5. 已知一多边形的每一个内角都等于150°,则这个多边形是( )A、十二边形 B、十边形 C、八边形 D、六边形6. 如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( ) A、主视图 B、左视图 C、俯视图 D、主视图和左视图7. 如图,在平行四边形ABCD中,BD为对角线,点E、O、F分别是 AB、BD、BC的中点,且OE=3,OF=2,则平行四边形ABCD的周长为( )
A、主视图 B、左视图 C、俯视图 D、主视图和左视图7. 如图,在平行四边形ABCD中,BD为对角线,点E、O、F分别是 AB、BD、BC的中点,且OE=3,OF=2,则平行四边形ABCD的周长为( )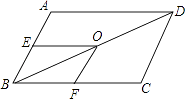 A、10 B、12 C、15 D、208. 有20个数据,其中8个数的平均数为11,另12个数的平均数是12,则这20个数的平均数是( )A、11.5 B、11.6 C、23.2 D、2329. 如图,AB与⊙O相切于点B,OA=2,∠OAB=30°,弦BC∥OA,则劣弧 的长是( )
A、10 B、12 C、15 D、208. 有20个数据,其中8个数的平均数为11,另12个数的平均数是12,则这20个数的平均数是( )A、11.5 B、11.6 C、23.2 D、2329. 如图,AB与⊙O相切于点B,OA=2,∠OAB=30°,弦BC∥OA,则劣弧 的长是( )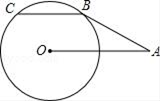 A、 B、 C、 D、10. 如图,平面直角坐标系中,矩形OABC的边与函数y= (x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
A、 B、 C、 D、10. 如图,平面直角坐标系中,矩形OABC的边与函数y= (x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( ) A、4 B、6 C、8 D、不能确定11. 如果多项式 ,则p的最小值是( )A、1005 B、1006 C、1007 D、100812. 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;② 2a>b;③b=a+c;④8a+c>0;⑤ax2+bx+c=0的两根分别为﹣3和1.其中正确的命题有( )
A、4 B、6 C、8 D、不能确定11. 如果多项式 ,则p的最小值是( )A、1005 B、1006 C、1007 D、100812. 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;② 2a>b;③b=a+c;④8a+c>0;⑤ax2+bx+c=0的两根分别为﹣3和1.其中正确的命题有( )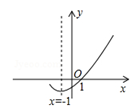 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每小题4分,共24分)
-
13. 计算:〡一 〡= .14. 当x时,分式 有意义.15. 若x2-9=(x-3)(x+a),则a= .16. 如图,在地面上离旗杆底部 米的 处,用测角仪测得旗杆顶端 的仰角为 ,若测角仪的高度为 米,则旗杆 的高为米.(结果保留根号)
 17. 如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=度.
17. 如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=度.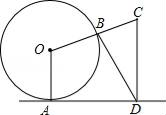 18. 如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于 .
18. 如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于 .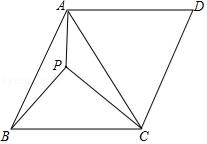
三、解答题(8小题,共78分)
-
19.(1)、计算: ;(2)、解不等式:20. 已知:抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).(1)、求此抛物线的表达式;(2)、如果此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.21. 如图,在▱ABCD中,AB⊥AC,AB=1,BC= ,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于E,F.
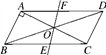 (1)、求BD的长;(2)、当旋转角∠AOF等于多少度时,△AOF与△BOE的面积相等?请写出理由.22. 某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽查部分学生做了一次问卷调查,要求学生选出自己最喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
(1)、求BD的长;(2)、当旋转角∠AOF等于多少度时,△AOF与△BOE的面积相等?请写出理由.22. 某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽查部分学生做了一次问卷调查,要求学生选出自己最喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下: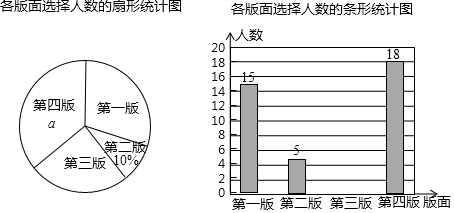
请根据图中信息,解答下列问题:
(1)、该调查的样本容量为 , ,“第一版”对应扇形的圆心角为 ;(2)、请你补全条形统计图;
(3)、若该校有1000名学生,请你估计全校学生中最喜欢“第三版”的人数.
23. 如图,在等边△ABC 内有一点D,AD=5,BD=6,CD=4,将线段AD绕点A旋转到AE,使∠DAE=∠BAC,连接EC.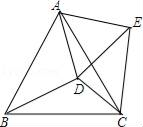 (1)、求CE的长;(2)、求cos∠CDE的值.24. 某商家用1200元购进了一批T恤,上市后很快售完,商家又用2800元购进了第二批这种T恤,所购数量是第一批购进量的2倍,但单价贵了5元.(1)、该商家购进的第一批T恤是多少件?(2)、若两批T恤按相同的标价销售,最后剩下20件按八折优惠卖出,如果希望两批T恤全部售完的利润率不低于16%(不考虑其它因素),那么每件T恤的标价至少是多少元?25. 如图(1),P 为△ABC 所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点 P 叫做△ABC 的费马点.
(1)、求CE的长;(2)、求cos∠CDE的值.24. 某商家用1200元购进了一批T恤,上市后很快售完,商家又用2800元购进了第二批这种T恤,所购数量是第一批购进量的2倍,但单价贵了5元.(1)、该商家购进的第一批T恤是多少件?(2)、若两批T恤按相同的标价销售,最后剩下20件按八折优惠卖出,如果希望两批T恤全部售完的利润率不低于16%(不考虑其它因素),那么每件T恤的标价至少是多少元?25. 如图(1),P 为△ABC 所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点 P 叫做△ABC 的费马点.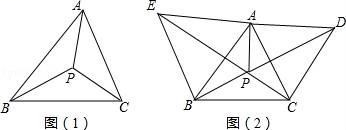 (1)、如果点 P 为锐角△ABC 的费马点,且∠ABC=60°.
(1)、如果点 P 为锐角△ABC 的费马点,且∠ABC=60°.①求证:△ABP∽△BCP;
②若 PA=3,PC=4,求PB
(2)、已知锐角△ABC,分别以 AB、AC 为边向外作正△ABE 和正△ACD,CE 和 BD相交于 P 点.如图(2)①求∠CPD 的度数;
②求证:P 点为△ABC 的费马点.
26. 如图, 是 的直径, AB是 的一条弦, , 的延长线交 于点 、交 的延长线于点 ,连接 且恰好 ∥ ,连接 交 于点 ,延长 交 于点 ,连接 .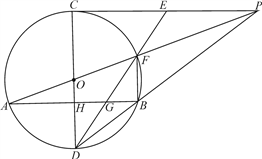 (1)、求证: 是 的切线;(2)、求证: ;
(1)、求证: 是 的切线;(2)、求证: ;
(3)、当 时,求 的值.