北师大版2019年中考数学最新仿真猜押卷（四）
试卷更新日期：2019-04-29 类型：中考模拟
一、单选题：(共10题，30分）
-
1. 下面四个汽车标志图案中是中心对称图形的是（ ）A、
B、
C、
D、
2. ﹣1的绝对值是（ ）A、﹣1 B、1 C、0 D、±13. 斑叶兰被列为国家二级保护植物，它的一粒种子重约0.0000005克．将0.0000005用科学记数法表示为（ ）
A、5×107 B、5×10﹣7 C、0.5×10﹣6 D、5×10﹣64. 如图，在△ABC中，∠C=90°，AB=5，BC=3，则sinA的值是（ ）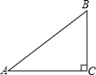
A、 B、 C、 D、5.如图△ABC中，D、E分别是边AB、AC的中点，已知DE=5，则BC的长为（ ）
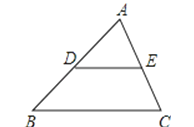A、8 B、9 C、10 D、116. 如图，一个圆形转盘被分成6个圆心角都为60°的扇形，任意转动这个转盘1次，当转盘停止转动时，指针指向阴影区域的概率是（ ）
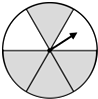A、 B、 C、 D、7. 七（1）班的6位同学在一节体育课上进行引体向上训练时，统计数据分别为7，12，10，6，9，6则这组数据的中位数是（ ）A、6 B、7 C、8 D、98. 下列函数中，当x＞0时，y值随x值的增大而减小的是（ ）A、y=x B、y=2x﹣1 C、y= D、y=x29. 已知：如图，⊙O是△ABC的外接圆，D为CB延长线上一点，∠AOC=130°，则∠ABD的度数为（ ）
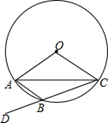A、40° B、50° C、65° D、100°二、填空题：(共6题，24分）
-
10. 分解因式：ax2﹣ay2= ．11. 如图，数轴上点A表示的数为a，化简：a+ = ．
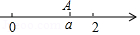12. 如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是边BM、CM的中点，当AB：AD=时，四边形MENF是正方形．
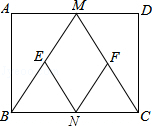13. 把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB=3cm，BC=5cm，则重叠部分△DEF的面积是 cm2 ．
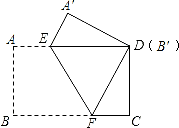14. 如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C= ．
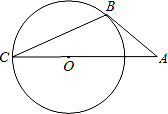15. 如图1，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A′B′D′的位置，得到图2，则阴影部分的周长为 ．
三、解答题：(共9题，66分）
-
16. 解方程组17. 先化简：（1﹣ ）• ，再从1，2，3中选取的一个合适的数代入求值．18. 如图，在Rt△ABC中，∠ACB=90°．
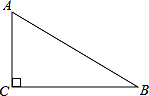(1)、用尺规在边BC上求作一点P，使PA=PB（不写作法，保留作图痕迹）(2)、连结AP，当∠B为度时，AP平分∠CAB．19. 如图，在东西方向的海岸线l上有一长为1千米的码头MN，在码头西端M的正西方向30 千米处有一观察站O．某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向，且与O相距 千米的A处；经过40分钟，又测得该轮船位于O的正北方向，且与O相距20千米的B处．
(1)、求该轮船航行的速度；(2)、如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸？请说明理由．（参考数据： ， ）20. 我市中小学全面开展“阳光体育”活动，某校在大课间中开设了A：体操，B：跑操，C：舞蹈，D：健美操四项活动，为了解学生最喜欢哪一项活动，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：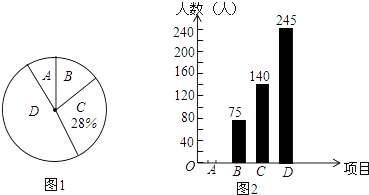
(1)、这次被调查的学生共有 人．(2)、请将统计图2补充完整．(3)、统计图1中B项目对应的扇形的圆心角是 度．(4)、已知该校共有学生3600人，请根据调查结果估计该校喜欢健美操的学生人数．21. 如图，▱ABCD的对角线AC，BD相交于点O．E，F是AC上的两点，并且AE=CF，连接DE，BF．
(1)、求证：△DOE≌△BOF；(2)、若BD=EF，连接FB，DF．判断四边形EBFD的形状，并说明理由．22. 如图，抛物线y=ax2+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A、B两点，与y轴交于点C，且BO=OC=3AO，直线y=﹣ x+1与y轴交于点D．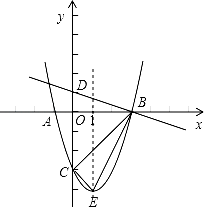
(1)、求抛物线的解析式；(2)、证明：△DBO∽△EBC；(3)、在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请直接写出符合条件的P点坐标，若不存在，请说明理由．23. 如图，AB，BC，CD分别与⊙O相切于E，F，G．且AB∥CD．BO=6cm，CO=8cm．
(1)、求证：BO⊥CO；(2)、求BE和CG的长．24. 如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2.5）．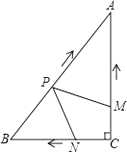
(1)、当t为何值时，以A，P，M为顶点的三角形与△ABC相似？(2)、是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．