北师大版2019年中考数学最新仿真猜押卷(五)
试卷更新日期:2019-04-29 类型:中考模拟
一、选择题(每小题3分,共30分)
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 4的倒数是( )A、 B、 C、 D、3. 震惊世界的MH370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中,首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为( )A、4.5×102 B、4.5×103 C、45.0×102 D、0.45×1044. 若代数式x+2的值为1,则x等于( )A、1 B、﹣1 C、3 D、﹣35. 不等式组 的解集在数轴上表示为( )
2. 4的倒数是( )A、 B、 C、 D、3. 震惊世界的MH370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中,首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为( )A、4.5×102 B、4.5×103 C、45.0×102 D、0.45×1044. 若代数式x+2的值为1,则x等于( )A、1 B、﹣1 C、3 D、﹣35. 不等式组 的解集在数轴上表示为( )
A、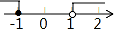 B、
B、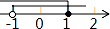 C、
C、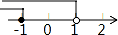 D、
D、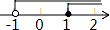 6. 函数y= 中,自变量x的取值范围是( )A、x≥﹣5 B、x≤﹣5 C、x≥5 D、x≤57. 某校开展为“希望小学”捐书活动,以下是八名学生捐书的册数:2,3,2,2,6,7,6,5,则这组数据的中位数为( )A、4 B、4.5 C、3 D、28. 一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的概率为( )A、 B、 C、 D、9. 若两个相似多边形的面积之比为1:4,则它们的周长之比为( )A、1:4 B、1:2 C、2:1 D、1:1610. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确结论的个数是( )
6. 函数y= 中,自变量x的取值范围是( )A、x≥﹣5 B、x≤﹣5 C、x≥5 D、x≤57. 某校开展为“希望小学”捐书活动,以下是八名学生捐书的册数:2,3,2,2,6,7,6,5,则这组数据的中位数为( )A、4 B、4.5 C、3 D、28. 一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的概率为( )A、 B、 C、 D、9. 若两个相似多边形的面积之比为1:4,则它们的周长之比为( )A、1:4 B、1:2 C、2:1 D、1:1610. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确结论的个数是( )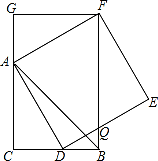 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题:(共6题,24分)
-
11. 9的算术平方根是 , = , ﹣ = .12. 方程3x+1=7的根是 .13. 如图,已知函数y=x-2和y=-2x+1的图象交于点P,根据图象可得方程组 的解是 .
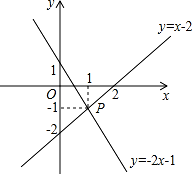 14. 100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是 .15. 如左下图,已知Rt△ABC中,斜边BC上的高AD=4,cosB= ,则AC= .
14. 100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是 .15. 如左下图,已知Rt△ABC中,斜边BC上的高AD=4,cosB= ,则AC= .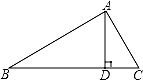 16. 如右下图,在Rt△ABC中,∠ABC=90°,AB=BC= ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
16. 如右下图,在Rt△ABC中,∠ABC=90°,AB=BC= ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
三、问答题:(共1题,6分)
-
17. 先化简,再求值: + ,其中a= ﹣1,b= .
四、综合题:(共8题,60分)
-
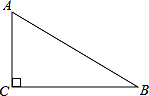
18. 如图,在Rt△ABC中,∠ACB=90°.
 (1)、用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹)(2)、连结AP,当∠B为度时,AP平分∠CAB.19. 六•一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.(1)、求A、B两种品牌服装每套进价分别为多少元?(2)、该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?20. 2016年3月,我市某中学举行了“爱我中国•朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)、用尺规在边BC上求作一点P,使PA=PB(不写作法,保留作图痕迹)(2)、连结AP,当∠B为度时,AP平分∠CAB.19. 六•一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.(1)、求A、B两种品牌服装每套进价分别为多少元?(2)、该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?20. 2016年3月,我市某中学举行了“爱我中国•朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题: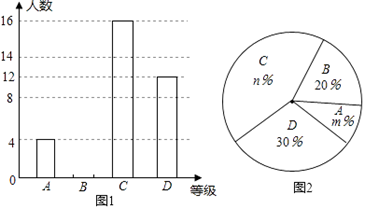 (1)、参加朗诵比赛的学生共有人,并把条形统计图补充完整;(2)、扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;(3)、学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.21. 菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)、参加朗诵比赛的学生共有人,并把条形统计图补充完整;(2)、扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;(3)、学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.21. 菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.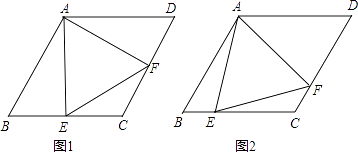 (1)、如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)、如图2,若∠EAF=60°,求证:△AEF是等边三角形.22. 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
(1)、如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)、如图2,若∠EAF=60°,求证:△AEF是等边三角形.22. 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.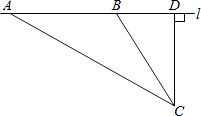 (1)、求AB的长(结果保留根号);(2)、已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据: ≈1.73, ≈1.41)23. 某公司销售A,B两种产品,根据市场调研,确定两条信息:信息1:销售A种产品所获利润y:(万元)与销售产品x(吨)之间存在二次函数关系,如图所示:信息2:销售B种产品所获利润y(万元)与销售产品x(吨)之间存在正比例函数关系y2=0.3x.根据以上信息,解答下列问题;
(1)、求AB的长(结果保留根号);(2)、已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据: ≈1.73, ≈1.41)23. 某公司销售A,B两种产品,根据市场调研,确定两条信息:信息1:销售A种产品所获利润y:(万元)与销售产品x(吨)之间存在二次函数关系,如图所示:信息2:销售B种产品所获利润y(万元)与销售产品x(吨)之间存在正比例函数关系y2=0.3x.根据以上信息,解答下列问题; (1)、求二次函数解析式;(2)、该公司准备购进A、B两种产品共10吨,求销售A、B两种产品获得的利润之和最大是多少万元.24. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= .
(1)、求二次函数解析式;(2)、该公司准备购进A、B两种产品共10吨,求销售A、B两种产品获得的利润之和最大是多少万元.24. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= .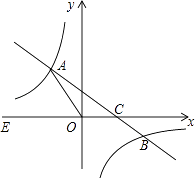 (1)、求该反比例函数和一次函数的解析式;(2)、求△AOC的面积;(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.25. 如图,在直角坐标系中,⊙M经过原点O(0,0),点A( ,0)与点B(0,﹣ ),点D在劣弧 上,连接BD交x轴于点C,且∠COD=∠CBO.
(1)、求该反比例函数和一次函数的解析式;(2)、求△AOC的面积;(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.25. 如图,在直角坐标系中,⊙M经过原点O(0,0),点A( ,0)与点B(0,﹣ ),点D在劣弧 上,连接BD交x轴于点C,且∠COD=∠CBO. (1)、求⊙M的半径;(2)、求证:BD平分∠ABO;(3)、在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.
(1)、求⊙M的半径;(2)、求证:BD平分∠ABO;(3)、在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.
-