北师大版2019年中考数学最新仿真猜押卷(三)
试卷更新日期:2019-04-29 类型:中考模拟
一、单选题:(共10题,30分)
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 首届中国(北京)国际服务贸易交易会(京交会)于2012年6月1日闭幕,本届京交会期间签订的项目成交总金额达60 110 000 000美元.将60 110 000 000用科学记数法表示应为( )A、6.011×109 B、60.11×109 C、6.011×1010 D、0.6011×10113. ﹣5的绝对值是( )A、5 B、﹣5 C、 D、﹣4. 下列计算,正确的是( )A、(﹣2)﹣2=4 B、 C、46÷(﹣2)6=64 D、5. 若分式 的值为0,则x的值为( )A、﹣2 B、0 C、2 D、±26. 实数a在数轴上的位置如图所示,则|a﹣2.5|=( )
2. 首届中国(北京)国际服务贸易交易会(京交会)于2012年6月1日闭幕,本届京交会期间签订的项目成交总金额达60 110 000 000美元.将60 110 000 000用科学记数法表示应为( )A、6.011×109 B、60.11×109 C、6.011×1010 D、0.6011×10113. ﹣5的绝对值是( )A、5 B、﹣5 C、 D、﹣4. 下列计算,正确的是( )A、(﹣2)﹣2=4 B、 C、46÷(﹣2)6=64 D、5. 若分式 的值为0,则x的值为( )A、﹣2 B、0 C、2 D、±26. 实数a在数轴上的位置如图所示,则|a﹣2.5|=( )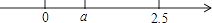 A、a﹣2.5 B、2.5﹣a C、a+2.5 D、﹣a﹣2.57. 下列函数中,当x>0时,y值随x值的增大而减小的是( )A、y=x B、y=2x﹣1 C、y= D、y=x28. 某校开展为“希望小学”捐书活动,以下是八名学生捐书的册数:2,3,2,2,6,7,6,5,则这组数据的中位数为( )A、4 B、4.5 C、3 D、29. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
A、a﹣2.5 B、2.5﹣a C、a+2.5 D、﹣a﹣2.57. 下列函数中,当x>0时,y值随x值的增大而减小的是( )A、y=x B、y=2x﹣1 C、y= D、y=x28. 某校开展为“希望小学”捐书活动,以下是八名学生捐书的册数:2,3,2,2,6,7,6,5,则这组数据的中位数为( )A、4 B、4.5 C、3 D、29. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )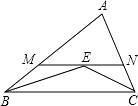 A、6 B、7 C、8 D、910. 如图,已知⊙O过正方形ABCD的顶点A,B,且与CD边相切,若正方形的边长为2,则圆的半径为( )
A、6 B、7 C、8 D、910. 如图,已知⊙O过正方形ABCD的顶点A,B,且与CD边相切,若正方形的边长为2,则圆的半径为( )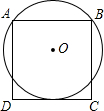 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题:(共6题,24分)
-
11. 若代数式 有意义,则x的取值范围是12. 已知 ,则 = .13. 方程x﹣5=0的解是x= .14. 若A(x1 , y1)和B(x2 , y2)在反比例函数 的图象上,且0<x1<x2 , 则y1与y2的大小关系是y1y2 .15. 如左下图,在△ABC中,D、E分别是AB、AC的中点,若BC=10,则DE= .
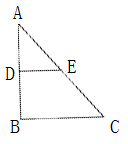 16. 如右上图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B'C,则在旋转过程中点A、C′两点间的最大距离是 .
16. 如右上图,在△ABC中,∠C=90°,AC=3,BC=4,点O是BC中点,将△ABC绕点O旋转得△A′B'C,则在旋转过程中点A、C′两点间的最大距离是 .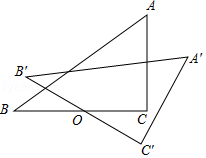
三、综合题:(共6题,41分)
-
17. 计算
|﹣2|﹣(﹣ )0+( )-1
18. 已知平行四边形ABCD.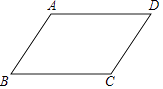 (1)、尺规作图:作∠BAD的平分线交直线BC于点E,交DC延长线于点F(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,求证:CE=CF.19. 如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y= (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(1)、尺规作图:作∠BAD的平分线交直线BC于点E,交DC延长线于点F(要求:尺规作图,保留作图痕迹,不写作法);(2)、在(1)的条件下,求证:CE=CF.19. 如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y= (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.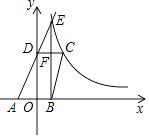 (1)、若EB= OD,求点E的坐标;(2)、若四边形ABCD为平行四边形,求过A、D两点的函数关系式.20. 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,AE∥CD,CE∥AB,判断四边形ADCE的形状,并证明你的结论.
(1)、若EB= OD,求点E的坐标;(2)、若四边形ABCD为平行四边形,求过A、D两点的函数关系式.20. 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,AE∥CD,CE∥AB,判断四边形ADCE的形状,并证明你的结论.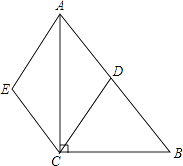 21. 深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图中提供的信息,解答下列问题:
21. 深圳市某校艺术节期间,开展了“好声音”歌唱比赛,在初赛中,学生处对初赛成绩做了统计分析,绘制成如下频数、频率分布表和频数分布直方图(如图),请你根据图中提供的信息,解答下列问题: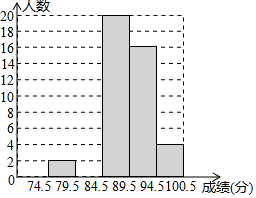
分组
频数
频率
74.5≤x<79.5
2
0.04
79.5≤x<84.5
a
0.16
84.5≤x<89.5
20
0.40
89.5≤x<94.5
16
0.32
94.5≤x<100.5
4
b
合计
50
1
(1)、频数、频率分布表中a= , b=;(2)、补全频数分布直方图;(3)、初赛成绩在94.5≤x<100.5分的四位同学恰好是七年级、八年级各一位,九年级两位,学生处打算从中随机挑选两位同学谈一下决赛前的训练,则所选两位同学恰好都是九年级学生的概率为 .22. 一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62米,到达D点,在测得山顶点A的仰角为60°(B、C、D三点在同一水平面上,且测量仪的高度忽略不计).求小岛高度AC(结果精确的1米,参考数值: )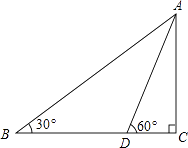 23. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
23. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.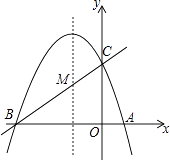 (1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)、设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.24. 如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交 于点F,交过点C的切线于点D.
(1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)、设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.24. 如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交 于点F,交过点C的切线于点D.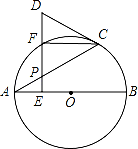 (1)、求证:DC=DP;(2)、若∠CAB=30°,当F是 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.25. 如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)、求证:DC=DP;(2)、若∠CAB=30°,当F是 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.25. 如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.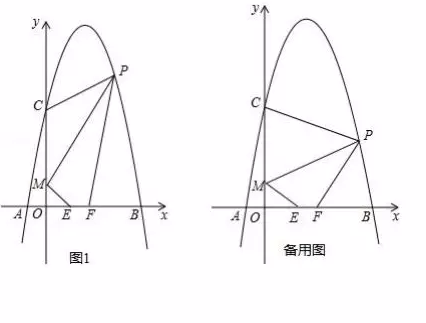 (1)、求此抛物线的解析式.(2)、当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.(3)、若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
(1)、求此抛物线的解析式.(2)、当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.(3)、若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.