北师大版2019年中考数学最新仿真猜押卷（二）

试卷更新日期：2019-04-29 类型：中考模拟

进入出卷网下载

一、单选题：(共10题，30分）

1. -2的绝对值是（）

A、 $- \frac{1}{2}$ B、－2 C、 $\frac{1}{2}$ D、2

查看试题解析
2. 未来三年，国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题．将8450亿元用科学记数法表示为（　　）

A、0.845×10⁴亿元 B、8.45×10³亿元 C、8.45×10⁴亿元 D、84.5×10²亿元

查看试题解析
3. 下列计算，正确的是（）

A、 ${(- 2)}^{- 2} = 4$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $4^{6} \div {(- 2)}^{6} = 64$ D、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$

查看试题解析
4. 不等式组 ${\begin{matrix} x + 1 > 0 \\ 1 - \frac{1}{3} x > 0 \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 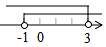B、 C、 D、

查看试题解析
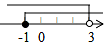5. 方程2x﹣1=3的解是（）

A、﹣1 B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
6. 一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9，这5个数据的中位数是（　　）.

A、6 B、7 C、8 D、9

查看试题解析
7. 圆锥的主视图是边长为4cm的等边三角形，则该圆锥俯视图的面积是（）

A、4πcm² B、8πcm² C、12πcm² D、16πcm²

查看试题解析
8. 正方形的一条对角线长为4，则这个正方形的面积是（）

A、8 B、4 $\sqrt{2}$ C、8 $\sqrt{2}$ D、16

查看试题解析
9. 如图，⊙O过点B，C．圆心O在等腰直角△ABC的内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（）

A、 $\sqrt{10}$ B、2 $\sqrt{3}$ C、3 $\sqrt{2}$ D、 $\sqrt{13}$

查看试题解析
10.
如图，在矩形ABCD中，AB=6cm，BC=4cm．动点E从点B出发，沿着线路BC→CD→DA运动，在BC段的平均速度是1cm/s，在CD段的平均速度是2cm/s，在DA段的平均速度是4cm/s，到点A停止．设△ABE的面积为y（cm²），则y与点E的运动时间t（s）的函数关系图象大致是（）

A、 B、 C、 D、

查看试题解析

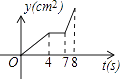
二、填空题：(共6题，24分）

11. 在△ABC中，∠BAC=90°，AB=3，AC=4．AD平分∠BAC交BC于D，则BD的长为．

查看试题解析
12. 分解因式：a²﹣ab= ．

查看试题解析
13. 某种商品每件的标价为240元，按标价的八折销售时，每件仍能获利20%，则这种商品每件的进价为元．

查看试题解析
14. 若 $\frac{a}{b} = \frac{1}{2}$ ，则 $\frac{a + b}{b}$ = ．

查看试题解析
15. 如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交 $\overset{⌢}{A B}$ 于点E，以点O为圆心，OC的长为半径作 $\overset{⌢}{C D}$ 交OB于点D．若OA=2，则阴影部分的面积为．

查看试题解析

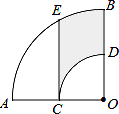
三、解答题

16. 计算
$\frac{1}{2}$ ^（-1）+ $\sqrt{2}$ cos45°﹣ $\sqrt[3]{27}$ ；

查看试题解析
17. 如图，在Rt△ABC中，∠ACB=90°．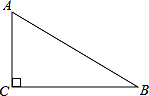

(1)、用尺规在边BC上求作一点P，使PA=PB（不写作法，保留作图痕迹）

(2)、连结AP，当∠B为度时，AP平分∠CAB．

查看试题解析
18. 马小虎的家距离学校1800米，一天马小虎从家去上学，出发10分钟后，爸爸发现他的数学课本忘记拿了，立即带上课本去追他，在距离学校200米的地方追上了他，已知爸爸的速度是马小虎速度的2倍，求马小虎的速度．
查看试题解析
19. 如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，

(1)、求证：∠DHO=∠DCO．

(2)、若OC=4，BD=6，求菱形ABCD的周长和面积．

查看试题解析
20. 某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目，要求毎位学生必须且只需选考其中一项，该市东风中学初三（2）班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示．

(1)、求该班的学生人数；

(2)、若该校初三年级有1000人，估计该年级选考立定供远的人数．

查看试题解析
21. 某机动车出发前油箱内有油42升，行驶若干小时后，途中在加油站加油若干升，油箱中余油量Q升与行驶时间t小时之间的函数关系如图所示.请回答以下问题：

(1)、机动车行驶几小时后加油？

(2)、求加油前油箱余油量Q与行驶时间t的函数关系式.

(3)、中途加油多少升？

查看试题解析

四、综合题：(共3题，27分）

22. 如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为E，射线EP交 $\overset{⌢}{A C}$ 于点F，交过点C的切线于点D．

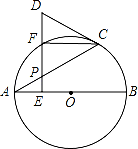(1)、求证：DC=DP；

(2)、若∠CAB=30°，当F是 $\overset{⌢}{A C}$ 的中点时，判断以A，O，C，F为顶点的四边形是什么特殊四边形？说明理由．

查看试题解析
23. 如图，在一次户外研学活动中，老师带领学生去测一条东西流向的河流的宽度（把河两岸看做平行线，河宽即两岸之间的垂线段的长度）．某同学在河南岸A处观测到河对岸水边有一棵树P，测得P在A北偏东60°方向上，沿河岸向东前行20米到达B处，测得P在B北偏东45°方向上．求河宽（结果保留一位小数． $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）．

查看试题解析
24. 如图已知：直线y=﹣x+3交x轴于点A，交y轴于点B，抛物线y=ax²+bx+c经过A、B、C（1，0）三点．

(1)、求抛物线的解析式；

(2)、若点D的坐标为（﹣1，0），在直线y=﹣x+3上有一点P，使△ABO与△ADP相似，求出点P的坐标；

(3)、在（2）的条件下，在x轴下方的抛物线上，是否存在点E，使△ADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．

查看试题解析