2018-2019学年初中数学北师大版八年级下册6.3三角形的中位线 同步练习

试卷更新日期：2019-04-29 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如图，在四边形ABCD中，∠C＝90°，E，F分别为AB，AD的中点，BC＝2，CD＝ 32 ，则EF的长为（   ）

    A、52 B、54 C、52 D、54

    查看试题解析

  • 2. 如图，在四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从点C向点D移动而点R不动时，下列结论成立的是（ ）

    A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不变 D、线段EF的长与点P的位置有关

    查看试题解析

  • 3. 如图，在四边形ABCD中，已知AB＝CD，M、N、P分别是AD、BC、BD的中点∠ABD＝20°，∠BDC＝70°，则∠NMP的度数为（   ）

    A、50° B、25° C、15° D、20

    查看试题解析

  • 4. 如图，在Rt△ABC中，∠C=90°，BC=4，AC=8，点D是AC上一个动点，以AB为对角线的所有平行四边形ADBE中，线段DE的最小值是（    ）

    A、4 B、 2 5 C、2 D、6

    查看试题解析

  • 5. 如图，在△ABC中，点M，N分别是AB，AC的中点，延长CB至点D，使MN=BD，连接DN，若CD=6，则MN的长为（    ）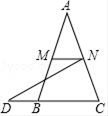

    A、2 B、3 C、4 D、6

    查看试题解析

  • 6. 如图，D，E为△ABC两边AB，AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=55 °，则∠BDF等于（  ）

    A、55° B、60° C、70° D、90°

    查看试题解析

  • 7. 如图，在梯形 ABCD 中， AB∥CD ，中位线 EF 与对角线 AC ， BD 交于 M ， N 两点，若 EF=18 cm， MN=8 cm，则 AB 的长等于（ ）

    A、10 cm B、13 cm C、20 cm D、26 cm

    查看试题解析

  • 8. 三角形的三条中位线的长分别为3 cm，4 cm，5 cm，则原三角形的周长为（ ）
    A、6.5 cm B、24 cm C、26 cm D、52 cm

    查看试题解析

  • 9. 如图，已知E，F，G，H分别为四边形ABCD各边的中点，若AC=10 cm，BD=12 cm，则四边形EFGH的周长为（ ）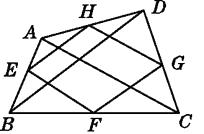

    A、10 cm B、11 cm C、12 cm D、22 cm

    查看试题解析

  • 10. 如图，梯形ABCD中，DC∥AB，EF是梯形的中位线，对角线BD交EF于G，若AB=10，EF=8，则GF的长等于（   ）

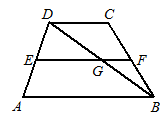    A、2 B、3 C、4 D、5

    查看试题解析

二、填空题

  • 11. 如图，在△ABC中，AB＝6，BC＝8，AC＝4，D、E、F分别为BC、AC、AB中点，连接DE、FE，则四边形BDEF的周长是 ．

    查看试题解析

  • 12. 如图，已知在△ABC 中，D、E 分别是 AB、AC 的中点，BC=6cm，则DE 的长度是 cm．

    查看试题解析

  • 13. 如图，在Rt△ABC中，∠ACB＝90°，点D，E分别是AB，AC的中点，点F是AD的中点．若AB＝8，则EF＝ ．

    查看试题解析

  • 14. 如图，在矩形ABCD中，AB＝1，BC＝7，将矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′，点E、F分别是BD、B′D′的中点，则EF的长度为cm．


    查看试题解析

  • 15. 在△A1B1C1中，已知A1B1＝7，B1C1＝4，A1C1＝5，依次连接△A1B1C1的三边中点，得△A2B2C2 ， 再依次连接△A2B2C2的三边中点得△A3B3C3 ， …，则△A5B5C5周长为.

    查看试题解析

  • 16. 如图，在▱ABCD中，对角线AC、BD相交于点O，点E、F分别是边AD、AB上的点，连结OE、OF、EF．若AB=7，BC=5 2 ，∠DAB=45°，则△OEF周长的最小值是 ．

    查看试题解析

三、解答题

  • 17. 如图，在△ABC中，已知AB=6，AC=10，AD平分∠BAC，BD⊥AD于点D，E为BC中点．求DE的长．

    查看试题解析

  • 18. 已知，如图在△ABC中，点D、E、F分别是BC、CA、AB边上的中点．

    求证：

    (1)、四边形AFDE是平行四边形；
    (2)、▱AFDE 周长等于AB+AC．

    查看试题解析

  • 19. 如图，已知△ABC中，D为AB的中点.

    (1)、请用尺规作图法作边AC的中点E，并连接DE（保留作图痕迹，不要求写作法）；
    (2)、在（1）条件下，若DE=4，求BC的长.

    查看试题解析

  • 20. 如图1：在等边△ABC中，点D，E分别在边AB，AC上，AD＝AE，连结BE，CD，点M、N、P分别是BE、CD、BC的中点．

    (1)、观察猜想

    图1中△PMN的形状是；

    (2)、探究证明

    把△ADE绕点A逆时针方向旋转到图2的位置，△PMN的形状是否发生改变？并说明理由．

    查看试题解析

  • 21. 在图1、图2中，线段AC=CE，点B是线段AC的中点，点D是线段CE的中点，四边形BCGF和CDHN都是正方形，AE的中点是M．如图1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，容易证明FM=MH，FM⊥HM；现将图1的CE绕点C顺时针旋转一个锐角，得到图2，判断△FMH的形状，并证明你的结论．

    查看试题解析

  • 22. △ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=α（0°＜α≤90°），点F，G，P分别是DE，BC，CD的中点，连接PF，PG．

       

    (1)、如图①，α=90°，点D在AB上，则∠FPG=°；
    (2)、如图②，α=60°，点D不在AB上，判断∠FPG的度数，并证明你的结论；
    (3)、连接FG，若AB=5，AD=2，固定△ABC，将△ADE绕点A旋转，则PF长度的最大值为；PF长度的最小值为；

    查看试题解析