2018-2019学年初中数学北师大版八年级下册6.2平行四边形的判定 同步练习
试卷更新日期：2019-04-29 类型：同步测试
一、单选题
-
1. 四边形ABCD中，对角线AC与BD交于点O，下列条件中不一定能判定这个四边形是平行四边形的是（ ）A、AB＝DC，∠ABC＝∠ADC B、AD∥BC，AB∥DC C、AB＝DC，AD＝BC D、OA＝OC，OB＝OD2. 已知：如图，四边形ABCD的两对角线AC，BD相交于点O，下列条件中，不能判定四边形ABCD是平行四边形的是（ ）
A、AB=CD，AD=BC B、AB∥CD，AD=BC C、AB∥CD，AD∥BC D、OA=OC，OB=OD3. 顺次连接平面上A，B，C，D四点得到一个四边形，从①AB∥CD，②BC＝AD，③∠A＝∠C，④∠B＝∠D四个条件中任取其中两个，可以得出“四边形ABCD是平行四边形”这一结论的情况共有（ ）A、5种 B、4种 C、3种 D、1种4. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，她带了两块碎玻璃，其编号应该是（ ）
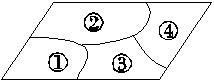A、①② B、①④ C、③④ D、②③5. 如图是某城市部分街道，已知AF∥BC，EC⊥BC，EF＝CF，BA∥DE，BD∥AE，甲、乙两人同时从B站乘车到F站，甲乘1路车，路线是B→A→E→F；乙乘2路车，路线是B→D→C→F.假设两车速度相同，途中耽误的时间相同，那么（ ）
A、甲将先到F站 B、乙将先到F站 C、甲、乙将同时到达 D、不能确定6. 在四边形ABCD中：①AB∥CD②AD∥BC③AB=CD④AD=BC，从以上选择两个条件使四边形ABCD为平行四边形的选法共有（ ）
A、3种 B、4种 C、5种 D、6种7. 下列不能判定一个四边形是平行四边形的是（ ）A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行另一组对边相等的四边形是平行四边形 D、对角线互相平分的四边形是平行四边形8.如图，点A是直线l外一点，在l上取两点B、C，分别以A、C为圆心，BC、AB长为半径画弧，两弧交于点D，分别连接AB、AD、CD，则四边形ABCD一定是（ ）
A、平行四边形 B、矩形 C、菱形 D、正方形9. 四边形ABCD的四个角∠A∶∠B∶∠C∶∠D满足下列哪一条件时，四边形ABCD是平行四边形（ ）A、1∶2∶2∶1 B、2∶1∶1∶1 C、1∶2∶3∶4 D、2∶1∶2∶110. 根据图中所给的边长长度及角度，判断下列选项中的四边形是平行四边形的为（ ）A、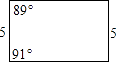
B、
C、
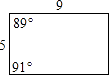D、
二、填空题
-
11. 把边长为3，5，7的两个全等三角形拼成四边形，一共能拼成种不同的四边形，其中有个平行四边形．12. 如图，在四边形ABCD中，AC、BD相交于点O，
(1)、若AB＝4cm，AD＝8cm，当BC＝cm，CD＝cm时，四边形ABCD为平行四边形；(2)、若BD＝8cm，AC＝10cm，当AO＝cm，DO＝cm时，四边形ABCD为平行四边形．13. 分别延长△ABC的边BA到点D，边CA到点E，使AD＝AB，AE＝AC，则四边形BCDE是 ， 其判断依据是 ．14. 如图，在△ABC中，∠BAC=90°，AB=4，AC=6，点D、E分别是BC、AD的中点，AF∥BC交CE的延长线于F．则四边形AFBD的面积为 ．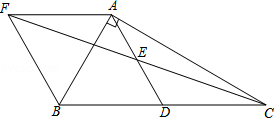
15. 如图，在平行四边形ABCD中，对角线交于点0，点E、F在直线AC上（不同于A、C），当E、F的位置满足的条件时，四边形DEBF是平行四边形．
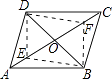16. 如图，在平行四边形ABCD中，EF∥AD，GH∥AB，EF、GH相交于点O，则图中共有个平行四边形.
三、解答题
-
17. 如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD，AD交BE于O．求证：AD与BE互相平分．
18. 已知：如图，▱ABCD的对角线AC，BD相交于0，点E，F分别在AO，CO上，且AE=CF，求证：四边形BEDF是平行四边形．
19. 如图，已知点E、F在四边形ABCD的对角线BD所在的直线上，且BE=DF，AE∥CF，请再添加一个条件（不要在图中再增加其它线段和字母），能证明四边形ABCD是平行四边形，并证明你的想法.你所添加的条件： ；
证明： .
20. 在△ABC中，AD是BC边上的中线，延长AD到点E，使DE＝AD，连结BE和CE，根据对角线互相平分的四边形是平行四边形，易得四边形ABEC是平行四边形．这种方法是数学证明中常用的一种添辅助线的方法，叫做“加倍中线法”．请用这种方法解决下面的问题：如图，在△ABC中，AB＝AC，延长AB到点D，使DB＝AB，E是AB的中点．求证：CD＝2CE.
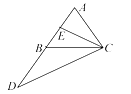21. 嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图所示的▱ABCD，并写出了如下尚不完整的已知和求证．
(1)、补全已知和求证（在方框中填空）；已知：如图，在四边形ABCD中，BC=AD，AB= ．
求证：四边形ABCD是四边形．
(2)、嘉琪同学想利用三角形全等，依据“两组对边分别平行的四边形是平行四边形”来证明．请你按她的想法完成证明过程．
22. 如图，四边形ABCD是矩形，∠EDC＝∠CAB，∠DEC＝90°.
(1)、求证：AC∥DE；(2)、过点B作BF⊥AC于点F，连结EF，试判断四边形BCEF的形状，并说明理由．23. 已知，如图，在平行四边形ABCD中，AC、BD相交于O点，点E、F分别为BO、DO的中点，连接AF，CE．
(1)、求证：四边形AECF是平行四边形；
(2)、如果E，F点分别在DB和BD的延长线上时，且满足BE=DF，上述结论仍然成立吗？请说明理由．
24. 如图，在四边形ABCD中，AD∥BC，AD=12cm，BC=15cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，点P，Q同时出发，设运动时间为t（s）．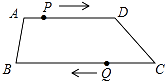
(1)、用含t的代数式表示：AP=；DP=；BQ=；CQ= ．
(2)、当t为何值时，四边形APQB是平行四边形？(3)、当t为何值时，四边形PDCQ是平行四边形？