2018-2019学年初中数学北师大版八年级下册6.1平行四边形的性质 同步练习
试卷更新日期：2019-04-29 类型：同步测试
一、单选题
-
1. 如图，在平行四边形ABCD中，AE平分∠DAB，∠AED＝26°，则∠C的度数为（ ）
A、26° B、42° C、52° D、56°2. 如图在▱ABCD中，已知AC=4cm，若△ACD的周长为13cm，则▱ABCD的周长为（ ）
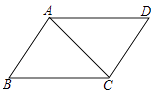A、26cm B、24cm C、20cm D、18cm3. 平行四边形的周长为25 ，对边的距离分别为2 、3 ，则这个平行四边形的面积为（ ）
A、15 2 B、25 2 C、30 2 D、50 24. 如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结OE．若∠ABC=60°，∠BAC=80°，则∠1的度数为（ ）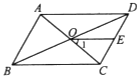
A、50° B、40° C、30° D、20°5. 如图，在▱ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则 ： 的值为
A、1：3 B、1：5 C、1：6 D、1：116. 如图，在▱ABCD中，AE⊥BC于点E，AF⊥CD于点F，若AE=20，CE=15，CF=7，AF=24，则BE的长为（ ）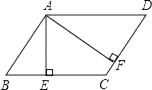
A、10 B、 C、15 D、7. 如图，在▱ABCD中，M是BC延长线上的一点，若∠A=125°，则∠MCD的度数是（ ）
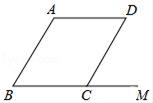A、45° B、65° C、55° D、75°8. 已知平行四边形ABCD中，∠A=4∠B，那么∠C等于（ ）A、36° B、45° C、135° D、144°9. 如图，在▱ABCD中，AB＝4，∠BAD的平分线与BC的延长线相交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG＝1，则AE的长为（ ）
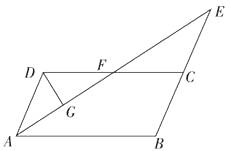A、2 B、4 C、4 D、810. 平行四边形ABCD中，∠A：∠B：∠C：∠D可能是（ ）A、2：1：2：1 B、1：2：2：1 C、2：1：1：2 D、1：2：3：4二、填空题
-
11. 已知平行四边形相邻两个内角相差40°，则该平行四边形中较小内角的度数是 ．12. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O，OE⊥BD交边AD于点E，若平行四边形ABCD的周长为20，则△ABE的周长等于 ．
13. 如图，E是平行四边形ABCD边BC上的一点，且AB＝BE，连接AE，AE的延长线与DC的延长线交于点F。若∠F＝70°，则∠D＝.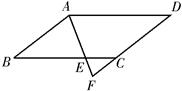
14. 如图，在平行四边形ABCD中，按以下步骤作图：①以点A为圆心，任意长为半径作弧，分别交AB，AD于点M，N；②分别以点M，N为圆心，以大于 MN的长为半径作弧，两弧相交于点P；③作射线AP交CD于点Q.若DQ＝2QC，BC＝3，则平行四边形ABCD的周长为.
15. 如图，在平行四边形ABCD中，AC＝8，BD＝6，AD＝a，则a的取值范围是.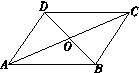
16. 如图，平行四边形ABCD的对角线相交于点O，且AD≠CD，过点O作OM⊥AC，交AD于点M.如果△CDM的周长为8，那么平行四边形ABCD的周长是.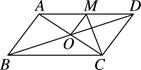
三、解答题
-
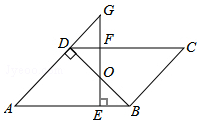
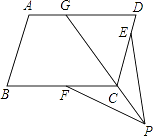
17. 如图，点G、E、F分别在平行四边形ABCD的边AD、DC和BC上，DG=DC，CE=CF，点P是射线GC上一点，连接FP，EP．
求证：FP=EP．
18. 如图，在▱ABCD中，点E、F分别在边CB、AD的延长线上，且BE＝DF，EF分别与AB、CD交于点G、H，求证：AG＝CH.
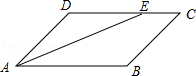
19. 已知：如图，在▱ABCD中，点E、F分别在BC、AD上，且AC、EF互相平分，求证：BE=DF．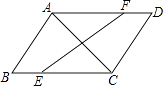
20. 如图，已知▱ABCD中，E为AD的中点，CE的延长线交BA的延长线于点E.
(1)、试说明线段CD与FA相等的理由；(2)、若使∠F＝∠BCF，▱ABCD的边长之间还需再添加一个什么条件？请你补上这个条件，并说明你的理由(不要再增添辅助线).
