2018-2019学年初中数学北师大版八年级下册5.3分式的加减法 同步练习
试卷更新日期:2019-04-29 类型:同步测试
一、单选题
-
1. 已知一辆汽车从甲地到乙地的速度为v1,从乙地原路返回到甲地的速度为v2,则这辆汽车来回的平均速度为 ( )A、 B、 C、 D、2. 已知a>b>0 , 的结果为( )A、0 B、正数 C、负数 D、不能确定3. 计算( ﹣ )÷ 的结果为( )A、
 B、
B、 C、
C、 D、
D、 4. 下列算式中,你认为正确的是( ).A、
4. 下列算式中,你认为正确的是( ).A、 B、1÷ . =l
C、
B、1÷ . =l
C、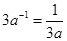 D、
D、 5. 已知 , ,则式子 的值是( )A、48 B、 C、16 D、126. 如果 ,那么代数式 的值是( )A、 B、 C、 D、17. 设有理数 都不为0,且 =0,则 的值为( )A、正数 B、负数 C、零 D、不能确定8. 把 , , 通分的过程中,不正确的是( )A、最简公分母是(x-2)(x+3)2 B、 C、 D、9. 若 ,则w=( )A、 B、 C、 D、10. 计算 得( )A、 B、 C、 D、2
5. 已知 , ,则式子 的值是( )A、48 B、 C、16 D、126. 如果 ,那么代数式 的值是( )A、 B、 C、 D、17. 设有理数 都不为0,且 =0,则 的值为( )A、正数 B、负数 C、零 D、不能确定8. 把 , , 通分的过程中,不正确的是( )A、最简公分母是(x-2)(x+3)2 B、 C、 D、9. 若 ,则w=( )A、 B、 C、 D、10. 计算 得( )A、 B、 C、 D、2二、填空题
-
11. 对分式 、 、 进行通分,确定的最简公分母应是 .12. 计算 的结果是 .13. 化简; ÷( ﹣1)= .
14. 已知x2-4x+4与 互为相反数,则式子 ÷(x+y)的值为 .15. 已知实数a,b,c满足 ,则 .16. 在小学阶段,我们知道可以将一个分数拆分成两个分数的和(差)的形式,例如 , = .类似地,我们也可以把一个较复杂的分式拆分成两个较简单,并且分子次数小于分母次数的分式的和或者差的形式.例如 = ,仿照上述方法,若分式 可以拆分成 的形式,那么(B+1)-(A+1)= .三、综解答题
-
17. 直接写出下列各组分式的最简公分母:(1)、 , , ;(2)、 , , ;(3)、 ;(4)、 .18. 计算:(1)、(2)、(3)、(4)、19. 化简求值:
 ,并从0,-1,2中选一个合适的数作为a的值代入求值。 20. 某学生化简分式 出现了错误,解答过程如下:
,并从0,-1,2中选一个合适的数作为a的值代入求值。 20. 某学生化简分式 出现了错误,解答过程如下:原式= (第一步)
= (第二步)
= .(第三步)
(1)、该学生解答过程是从第步开始出错的,其错误原因是;
(2)、请写出此题正确的解答过程.