江苏省南通、扬州、泰州、苏北四市七市2019届高三数学第一次（2月)模拟试卷

试卷更新日期：2019-04-29 类型：高考模拟

进入出卷网下载

一、填空题

1. 已知集合 $A = {1 ， 3}$ ， $B = {0 ， 1}$ ，则集合 $A \cup^{} B$ = ．

查看试题解析
2. 已知复数 $z = \frac{2 i}{1 - i} - 3 i$ （i为虚数单位），则复数z的模为.

查看试题解析
3. 某中学组织学生参加社会实践活动，高二（1）班50名学生参加活动的次数统计如下：

次数

2

3

4

5

人数

20

15

10

5

则平均每人参加活动的次数为.

查看试题解析
4. 如图是一个算法流程图，则输出的b的值为．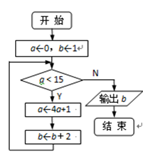

查看试题解析
5. 有数学、物理、化学三个兴趣小组，甲、乙两位同学各随机参加一个，则这两位同学参加不同兴趣小组的概率为．

查看试题解析
6. 已知正四棱柱的底面边长为 $3 cm$ ，侧面的对角线长是 $3 \sqrt{5} cm$ ，则这个正四棱柱的体积是 ${cm}^{3}$ ．

查看试题解析
7. 若实数 $x ， y$ 满足 $x \leq y \leq 2 x + 3$ ，则 $x + y$ 的最小值为．

查看试题解析
8. 在平面直角坐标系xOy中，已知抛物线 $y^{2} = 2 p x (p > 0)$ 的准线为l，直线l与双曲线 $\frac{x^{2}}{4} - y^{2} = 1$ 的两条渐近线分别交于A，B两点， $A B = \sqrt{6}$ ，则 $p$ 的值为．

查看试题解析
9. 在平面直角坐标系xOy中，已知直线 $y = 3 x + t$ 与曲线 $y = a sin x + b cos x (a ， b ， t \in R)$ 相切于点 $(0 ， 1)$ ，则 $(a + b) t$ 的值为．

查看试题解析
10. 已知数列 ${a_{n}}$ 是等比数列，有下列四个命题：
①数列 ${| a_{n} |}$ 是等比数列； ②数列 ${a_{n} a_{n + 1}}$ 是等比数列；

③数列 ${\frac{1}{a_{n}}}$ 是等比数列； ④数列 ${lg a_{n}^{2}}$ 是等比数列．

其中正确的命题有个．

查看试题解析
11. 已知函数 $f (x)$ 是定义在 $R$ 上的奇函数，且 $f (x + 2) = f (x)$ ．当 $0 < x \leq 1$ 时， $f (x) =$ $x^{3} - a x + 1$ ，则实数a的值为．

查看试题解析
12. 在平面四边形 $A B C D$ 中， $A B = 1 ， D A = D B$ ， $\overset{⇀}{A B} \cdot \overset{⇀}{A C} = 3 ， \overset{⇀}{A C} \cdot \overset{⇀}{A D} = 2 ，$ 则 $| \overset{⇀}{A C} + 2 \overset{⇀}{A D} |$ 的最小值为．

查看试题解析
13. 在平面直角坐标系xOy中，圆 $O ： x^{2} + y^{2} = 1$ ，圆 $C ： {(x - 4)}^{2} + y^{2} = 4$ ．若存在过点 $P (m ， 0)$ 的直线l，l被两圆截得的弦长相等，则实数m的取值范围是．

查看试题解析
14. 已知函数 $f (x) = (2 x + a) (| x - a | + | x + 2 a |) (a < 0)$ ．若 $f (1) + f (2) + f (3) +$ … $+ f (672) = 0$ ，则满足 $f (x) = 2019$ 的 $x$ 的值为．

查看试题解析

二、解答题

15. 如图，在四棱锥 $P - A B C D$ 中，M，N分别为棱PA，PD的中点．已知侧面PAD⊥底面ABCD，底面ABCD是矩形，DA=DP．

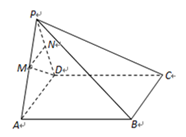(1)、求证： MN∥平面PBC；

(2)、求证： MD⊥平面PAB．

查看试题解析
16. 在△ABC中，a，b，c分别为角A，B，C所对边的长， $a cos B = \sqrt{2} b cos A$ ， $cos A = \frac{\sqrt{3}}{3}$ ．

(1)、求角 $B$ 的值；

(2)、若 $a = \sqrt{6}$ ，求△ABC的面积．

查看试题解析
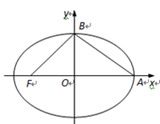17. 如图，在平面直角坐标系xOy中，椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的左焦点为 $F$ ，右顶点为 $A$ ，上顶点为 $B$ ．

(1)、已知椭圆的离心率为 $\frac{1}{2}$ ，线段 $A F$ 中点的横坐标为 $\frac{\sqrt{2}}{2}$ ，求椭圆的标准方程；

(2)、已知△ $A B F$ 外接圆的圆心在直线 $y = - x$ 上，求椭圆的离心率 $e$ 的值．

查看试题解析
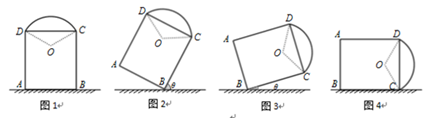18. 如图1，一艺术拱门由两部分组成，下部为矩形 $A B C D$ ， $A B ， A D$ 的长分别为 $2 \sqrt{3} m$ 和 $4 m$ ，上部是圆心为 $O$ 的劣弧 $C D$ ， $∠ C O D = \frac{2 π}{3}$ ．

(1)、求图1中拱门最高点到地面的距离；

(2)、现欲以B点为支点将拱门放倒，放倒过程中矩形 $A B C D$ 所在的平面始终与地面垂直，如图2、图3、图4所示．设 $B C$ 与地面水平线 $l$ 所成的角为 $θ$ ．记拱门上的点到地面的最大距离为 $h$ ，试用 $θ$ 的函数表示 $h$ ，并求出 $h$ 的最大值．

查看试题解析
19. 已知函数 $f (x) = \frac{a}{x} + ln x (a \in R)$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、设 $f (x)$ 的导函数为 $f^{'} (x)$ ，若 $f (x)$ 有两个不相同的零点 $x_{1} ， x_{2}$ ．
① 求实数 $a$ 的取值范围；

② 证明： $x_{1} f^{'} (x_{1}) + x_{2} f^{'} (x_{2}) > 2 ln a + 2$ ．

查看试题解析
20. 已知等差数列 ${a_{n}}$ 满足 $a_{4} = 4$ ，前8项和 $S_{8} = 36$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若数列 ${b_{n}}$ 满足 $\sum_{k = 1}^{n} (b_{k} a_{2 n + 1 - 2 k}) + 2 a_{n} = 3 (2^{n} - 1) ， (n \in N^{*})$ ．
① 证明： ${b_{n}}$ 为等比数列；

② 求集合 ${(m ， p) | \frac{a_{m}}{b_{m}} = \frac{3 a_{p}}{b_{p}} ， m ， p \in N^{*}}$ ．

查看试题解析
21. [选修4-2：矩阵与变换] 已知矩阵 $M = [\begin{matrix} a & b \\ c & d \end{matrix}]$ ， $N = [\begin{matrix} 1 & 0 \\ 0 & \frac{1}{2} \end{matrix}]$ ，且 ${(M N)}^{- 1} = [\begin{matrix} \frac{1}{4} & 0 \\ 0 & 2 \end{matrix}]$ ，求矩阵 $M$ ．

查看试题解析
22. [选修4-4：坐标系与参数方程] 在平面直角坐标系xOy中，曲线C的参数方程是 ${\begin{matrix} x = t \\ y = t^{2} \end{matrix}$ （ $t$ 为参数）．以原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程是 $ρ sin (θ - \frac{π}{4}) = \sqrt{2}$ ．

(1)、直线l的直角坐标方程；

(2)、直线 $l$ 被曲线C截得的线段长．

查看试题解析
23. [选修4-5：不等式选讲] 已知实数 $a ， b ， c$ 满足 $a^{2} + b^{2} + c^{2} \leq 1$ ，求证： $\frac{1}{a^{2} + 1} + \frac{1}{b^{2} + 1} + \frac{1}{c^{2} + 1} \geq \frac{9}{4}$ ．

查看试题解析
24. “回文数”是指从左到右与从右到左读都一样的正整数，如22，121，3553等．显然2位“回文数”共9个：11，22，33，…，99．现从9个不同2位“回文数”中任取1个乘以4，其结果记为X；从9个不同2位“回文数”中任取2个相加，其结果记为Y．

(1)、求X为“回文数”的概率；

(2)、设随机变量 $ξ$ 表示X，Y两数中“回文数”的个数，求 $ξ$ 的概率分布和数学期望 $E (ξ)$ ．

查看试题解析
25. 设集合 $B$ 是集合 $A_{n} = {1 ， 2 ， 3 ，$ …， $3 n - 2 ， 3 n - 1 ， 3 n} ， n \in N^{*}$ 的子集．记 $B$ 中所有元素的和为 $S$ （规定： $B$ 为空集时， $S$ =0）．若 $S$ 为3的整数倍，则称 $B$ 为 $A_{n}$ 的“和谐子集”．求：

(1)、集合 $A_{1}$ 的“和谐子集”的个数；

(2)、集合 $A_{n}$ 的“和谐子集”的个数．

查看试题解析

次数	2	3	4	5
人数	20	15	10	5