湖北省武汉市2019届高中毕业生理数二月调研测试试卷

试卷更新日期：2019-04-29 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知复数 $z$ 满足 $(3 + 4 i) z = 7 + i$ ，则 $z =$ （）

A、 $1 + i$ B、 $1 - i$ C、 $- 1 - i$ D、 $- 1 + i$

查看试题解析
2. 已知集合 $A = {x | x^{2} - 4 x \leq 0} ， B = {x | x 〉 0}$ ，则 $A \cap^{} B =$ （）

A、 $(0 ， 4]$ B、 $[0 ， 4]$ C、 $[0 ， 2]$ D、 $(0 ， 2]$

查看试题解析
3. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $a_{1} = 12 ， S_{5} = 90$ ，则等差数列 ${a_{n}}$ 的公差 $d =$ （）

A、2 B、 $\frac{3}{2}$ C、3 D、4

查看试题解析
4. 已知双曲线 $\frac{x^{2}}{4} - \frac{y^{2}}{b^{2}} = 1 (b > 0)$ 的渐近线方程为 $\sqrt{3} x \pm y = 0$ ，则 $b =$ （）

A、 $2 \sqrt{3}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{2}$ D、12

查看试题解析
5. 执行如图所示的程序框图，则输出 $s$ 的值为（）

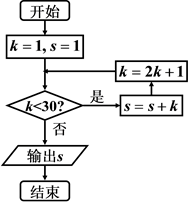A、5 B、12 C、27 D、58

查看试题解析
6. 如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（）

A、 $\frac{2 π}{3}$ B、 $\frac{4 π}{3}$ C、 $2 π$ D、 $2 \sqrt{5} π$

查看试题解析
7. 已知某口袋中装有2个红球，3个白球和1个蓝球，从中任取3个球，则其中恰有两种颜色的概率是（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{7}{20}$ D、 $\frac{13}{20}$

查看试题解析
8. 在 $△ A B C$ 中， $\overset{⇀}{A B} \cdot \overset{⇀}{A C} = 0 ， | \overset{⇀}{A B} | = 4 ， | \overset{⇀}{B C} | = 5 ， D$ 为线段 $B C$ 的中点， $E$ 为线段 $B C$ 垂直平分线 $l$ 上任一异于 $D$ 的点，则 $\overset{⇀}{A E} \cdot \overset{⇀}{C B} =$ （）

A、 $\frac{7}{2}$ B、 $\frac{7}{4}$ C、 $- \frac{7}{4}$ D、7

查看试题解析
9. 已知函数 $f (x) = 2 sin (ω x + \frac{π}{4})$ 在区间 $(0 ， \frac{π}{8})$ 上单调递增，则 $ω$ 的最大值为（）

A、 $\frac{1}{2}$ B、1 C、2 D、4

查看试题解析
10. 已知 $A ， B$ 为抛物线 $y^{2} = 4 x$ 上两点， $O$ 为坐标原点，且 $O A ⊥ O B$ ，则 $| A B |$ 的最小值为（）

A、 $4 \sqrt{2}$ B、 $2 \sqrt{2}$ C、8 D、 $8 \sqrt{2}$

查看试题解析
11. 若 $x ， y$ 满足约束条件 ${\begin{matrix} | x + 2 y | \leq 2 \\ | 2 y - 3 x | \leq 6 \end{matrix}$ ，则 $(x + 1) y$ 的取值范围为（）

A、 $[- 3 ， 0]$ B、 $[- 3 ， \frac{9}{4}]$ C、 $[0 ， \frac{9}{8}]$ D、 $[- 3 ， \frac{9}{8}]$

查看试题解析
12. 已知函数 $f (x) = e^{x} - a ln (a x - a) + a (a > 0)$ ，若关于 $x$ 的不等式 $f (x) > 0$ 恒成立，则实数 $a$ 的取值范围为（）

A、 $(0 ， e^{2}]$ B、 $(0 ， e^{2})$ C、 $[1 ， e^{2}]$ D、 $(1 ， e^{2})$

查看试题解析
13. $(x + 2) {(x - 2)}^{7}$ 展开式中 $x^{7}$ 项的系数为．

查看试题解析
14. 函数 $y = x ln (x + a)$ 在点 $(0 ， 0)$ 处的切线方程为 $y = x$ ，则实数 $a$ 的值为．

查看试题解析
15. 已知正项数列 ${a_{n}}$ 满足 $a_{1} = 1$ ，前 $n$ 项和 $S_{n}$ 满足 $4 S_{n} = {(a_{n - 1} + 3)}^{2} (n \geq 2 ， n \in N^{*})$ ，则数列 ${a_{n}}$ 的通项公式为 $a_{n} =$ ．

查看试题解析
16. 在棱长为1的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $A$ 关于平面 $B D C_{1}$ 的对称点为 $M$ ，则 $M$ 到平面 $A_{1} B_{1} C_{1} D_{1}$ 的距离为．

查看试题解析

二、解答题

17. 在 $△ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ．已知 $a = 2 ， b = 3 ， sin 2 C + sin A = 0$ ．

(1)、求 $c$ ；

(2)、求 $△ A B C$ 的面积．

查看试题解析
18. 如图，已知四边形 $A B C D$ 为梯形， $A B / / C D ， ∠ D A B = 90 ° ， B D D_{1} B_{1}$ 为矩形，平面 $B D D_{1} B_{1} ⊥$ 平面 $A B C D$ ，又 $A B = A D = B B_{1} = 1 ， C D = 2$ ．

(1)、证明： $C B_{1} ⊥ A D_{1}$ ；

(2)、求二面角 $B_{1} - A D_{1} - C$ 的余弦值．

查看试题解析

19. 一个工厂在某年连续10个月每月产品的总成本y（万元）与该月产量x（万件）之间有如下一组数据：

x	1.08	1.12	1.19	1.28	1.36	1.48	1.59	1.68	1.80	1.87
y	2.25	2.37	2.40	2.55	2.64	2.75	2.92	3.03	3.14	3.26

（答案均精确到0.001）

附注：①参考数据： $\sum_{i = 1}^{10} x_{i} = 14.45 ， \sum_{i = 1}^{10} y_{i} = 27.31$ ，

$\sqrt{\sum_{i = 1}^{10} x_{i}^{2} - 10 {\bar{x}}^{2}} = 0.850 ， \sqrt{\sum_{i = 1}^{10} y_{i}^{2} - 10 {\bar{y}}^{2}} = 1.042 ， \hat{b} = 1.222$ ，

②参考公式：相关系数 $r = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sqrt{(\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}) (\sum_{i = 1}^{n} y_{i}^{2} - n {\bar{y}}^{2})}}$ ，

回归方程 $\hat{y} = \hat{a} + \hat{b} x$ 中斜率和截距的最小二乘估计公式分别为： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}} ， \hat{a} = \bar{y} - \hat{b} \bar{x}$ ．

(1)、通过画散点图，发现可用线性回归模型拟合y与x的关系，请用相关系数加以说明；

(2)、①建立月总成本y与月产量x之间的回归方程；

②通过建立的y关于x的回归方程，估计某月产量为1.98万件时，此时产品的总成本为多少万元？

查看试题解析

20. 已知椭圆 $Γ ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的长轴长为4，离心率为 $\frac{\sqrt{2}}{2}$ ．

(1)、求椭圆 $Γ$ 的标准方程；

(2)、过 $P (1 ， 0)$ 作动直线 $A B$ 交椭圆 $Γ$ 于 $A ， B$ 两点， $Q$ 为平面上一点，直线 $Q A ， Q B ， Q P$ 的斜率分别为 $k_{1} ， k_{2} ， k_{0}$ ，且满足 $k_{1} + k_{2} = 2 k_{0}$ ，问 $Q$ 点是否在某定直线上运动，若存在，求出该直线方程；若不存在，请说明理由．

查看试题解析
21. 已知函数 $f (x) = (a x - x^{2}) e^{x} (a \geq 0)$ ．

(1)、若函数 $f (x)$ 在区间 $[2 ， + \infty)$ 上单调递减，求实数 $a$ 的取值范围；

(2)、设 $f (x)$ 的两个极值点为 $x_{1} ， x_{2} (x_{2} > x_{1})$ ，证明：当 $a \geq \frac{2 \sqrt{11}}{5}$ 时， $f (x_{1}) + f (x_{2}) > 0$ ．（附注： $ln 11 \approx 2.398$ ）

查看试题解析
22. 以坐标原点 $O$ 为极点， $x$ 轴正半轴为极轴，建立极坐标系，曲线 $C_{1} ： ρ^{2} - 4 ρ sin θ + 3 = 0$ ，曲线 $C_{2} ： ρ sin (θ - \frac{π}{4}) + \frac{\sqrt{2}}{2} = 0$ ．

(1)、求 $C_{1} ， C_{2}$ 的直角坐标方程；

(2)、已知曲线 $C_{1}$ 与 $y$ 轴交于 $A ， B$ 两点， $P$ 为 $C_{2}$ 上任一点，求 $| P A | + | P B |$ 的最小值．

查看试题解析
23. 已知函数 $f (x) = 2 | x + 1 | - | x - a | ， a \in R$ ．

(1)、当 $a = 1$ 时，求不等式 $f (x) > 0$ 的解集；

(2)、若关于 $x$ 的不等式 $f (x) \geq x$ 在 $x \in R$ 时恒成立，求实数 $a$ 的取值范围．

查看试题解析