河南省郑州市2019届高三理数第一次（1月)质量预测试卷

试卷更新日期：2019-04-29 类型：高考模拟

进入出卷网下载

一、单选题

1. 若复数 $\frac{1 + 2 a i}{2 - i} (a \in R)$ 的实部和虚部相等，则实数 $a$ 的值为 $($ 　　 $)$

A、1 B、 $- 1$ C、 $\frac{1}{6}$ D、 $- \frac{1}{6}$

查看试题解析
2. 已知集合 $M = {x | - 3 \leq x < 4}$ ， $N = {x | x^{2} - 2 x - 8 \leq 0}$ ，则 $($ 　　 $)$

A、 $M \cup^{} N = R$ B、 $M \cup^{} N = {x | - 3 \leq x < 4}$ C、 $M \cap^{} N = {x | - 2 \leq x \leq 4}$ D、 $M \cap^{} N = {x | - 2 \leq x < 4}$

查看试题解析
3. 已知矩形 $A B C D$ 中， $B C = 2 A B = 4$ ，现向矩形 $A B C D$ 内随机投掷质点 $M$ ，则满足 $\vec{M B} \cdot \vec{M C} \geq 0$ 的概率是 $($ 　　 $)$

A、 $\frac{π}{4}$ B、 $\frac{4 - π}{4}$ C、 $\frac{π}{2}$ D、 $\frac{π - 2}{4}$

查看试题解析
4. 下列函数既是奇函数，又在 $[- 1 ， 1]$ 上单调递增的是 $($ 　　 $)$

A、 $f (x) = | sin x |$ B、 $f (x) = ln \frac{e - x}{e + x}$ C、 $f (x) = \frac{1}{2} (e^{x} - e^{- x})$ D、 $f (x) = ln (\sqrt{x^{2} + 1} - x)$

查看试题解析
5. 在 $△ A B C$ 中，三边长分别为 $a ， a + 2$ ， $a + 4$ ，最小角的余弦值为 $\frac{13}{14}$ ，则这个三角形的面积为 $($ 　　 $)$

A、 $\frac{15}{4} \sqrt{3}$ B、 $\frac{15}{4}$ C、 $\frac{21}{4} \sqrt{3}$ D、 $\frac{35}{4} \sqrt{3}$

查看试题解析
6. 如图，在 $Δ A B C$ 中， $\overset{⇀}{A N} = \frac{2}{3} \overset{⇀}{N C}$ ， $P$ 是 $B N$ 上一点，若 $\overset{⇀}{A P} = t \overset{⇀}{A B} + \frac{1}{3} \overset{⇀}{A C}$ ，则实数 $t$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{1}{6}$ D、 $\frac{3}{4}$

查看试题解析
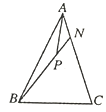7. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点分别为 $F_{1}$ ， $F_{2}$ ，实轴长为6，渐近线方程为 $y = \pm \frac{1}{3} x$ ，动点 $M$ 在双曲线左支上，点 $N$ 为圆 $E ： x^{2} + {(y + \sqrt{6})}^{2} = 1$ 上一点，则 $| M N | + | M F_{2} |$ 的最小值为（）

A、8 B、9 C、10 D、11

查看试题解析
8. 已知函数 $f (x) = sin (ω x + θ) (ω > 0 ， - \frac{π}{2} \leq θ \leq \frac{π}{2})$ 的图象相邻的两个对称中心之间的距离为 $\frac{π}{2}$ ，若将函数 $f (x)$ 的图象向左平移 $\frac{π}{6}$ 后得到偶函数 $g (x)$ 的图象，则函数 $f (x)$ 的一个单调递减区间为 $($ 　　 $)$

A、 $[- \frac{π}{3} ， \frac{π}{6}]$ B、 $[\frac{π}{4} ， \frac{7 π}{12}]$ C、 $[0 ， \frac{π}{3}]$ D、 $[\frac{π}{2} ， \frac{5 π}{6}]$

查看试题解析
9. 如图，网格纸上小正方形的边长为2，粗线画出的是某几何体的三视图，则该几何体的表面积为 $($ 　　 $)$

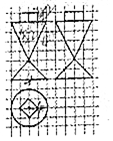A、 $16 \sqrt{2} + (32 + 16 \sqrt{2} + 16 \sqrt{5}) π$ B、 $16 \sqrt{2} + (16 + 16 \sqrt{2} + 16 \sqrt{5}) π$ C、 $16 \sqrt{2} + (32 + 32 \sqrt{2} + 32 \sqrt{5}) π$ D、 $16 \sqrt{2} + (16 + 32 \sqrt{2} + 32 \sqrt{5}) π$

查看试题解析
10. 已知直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中的底面为等腰直角三角形， $A B ⊥ A C$ ，点 $M ， N$ 分别是边 $A B_{1}$ ， $A_{1} C$ 上动点，若直线 $M N / /$ 平面 $B C C_{1} B_{1}$ ，点 $Q$ 为线段 $M N$ 的中点，则 $Q$ 点的轨迹为 $($ 　　 $)$

A、双曲线的一支 $($ 一部分 $)$ B、圆弧 $($ 一部分 $)$ C、线段 $($ 去掉一个端点 $)$ D、抛物线的一部分

查看试题解析
11. 物线 $x^{2} = 2 p y (p > 0)$ 的焦点为 $F$ ，已知点 $A ， B$ 为抛物线上的两个动点，且满足 $∠ A F B = 60^{\circ}$ ，过弦 $A B$ 的中点 $C$ 作该抛物线准线的垂线 $C D$ ，垂足为 $D$ ，则 $\frac{| \vec{A B} |}{| \vec{C D} |}$ 的最小值为 $($ 　　 $)$

A、 $\sqrt{3}$ B、1 C、 $\frac{2 \sqrt{3}}{3}$ D、2

查看试题解析
12. 已知函数 $f (x) = {\begin{cases} - 3 x^{2} + 6 x ， x \geq 0 \\ - x^{3} - 3 x^{2} + 4 ， x < 0 \end{cases}$ ，设 $A = {x \in Z | x (f (x) - a) \geq 0$ ，若 $A$ 中有且仅有4个元素，则满足条件的整数 $a$ 的个数为 $($ 　　 $)$

A、31 B、32 C、33 D、34

查看试题解析

二、填空题

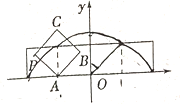
13. 已知 ${(\frac{1}{x} + x^{2})}^{n}$ 的展开式的各项系数和为64，则展开式中 $x^{3}$ 的系数为

查看试题解析
14. 已知变量 $x ， y$ 满足 ${\begin{matrix} x - 2 y + 4 \leq 0 \\ x \geq 2 \\ x + y - 6 \leq 0 \end{matrix}$ ，则 $z = \frac{y + 1}{x - 3}$ 的取值范围是

查看试题解析
15. 《中国诗词大会》（第三季）亮点颇多，在“人生自有诗意”的主题下，十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下，百人团齐声朗诵，别有韵味.若《沁园春·长沙》、《蜀道难》、《敕勒歌》、《游子吟》、《关山月》、《清平乐·六盘山》排在后六场，且《蜀道难》排在《游子吟》的前面，《沁园春·长沙》与《清平乐·六盘山》不相邻且均不排在最后，则后六场的排法有种．（用数字作答）

查看试题解析
16. 如图放置的边长为1的正方形 $P A B C$ 沿 $x$ 轴滚动，点 $B$ 恰好经过原点.设顶点 $P (x ， y)$ 的轨迹方程是 $y = f (x)$ ，则对函数 $y = f (x)$ 有下列判断：①函数 $y = f (x)$ 是偶函数；②对任意的 $x \in R$ ，都有 $f (x + 2) = f (x - 2)$ ；③函数 $y = f (x)$ 在区间 $[2 ， 3]$ 上单调递减；④函数 $y = f (x)$ 的值域是 $[0 ， 1]$ ；⑤ $\int_{0}^{2} f (x) d x = \frac{π + 1}{2}$ .其中判断正确的序号是．

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 为等比数列，首项 $a_{1} = 4$ ，数列 ${b_{n}}$ 满足 $b_{n} = {log}_{2} a_{n}$ ，且 $b_{1} + b_{2} + b_{3} = 12$ .
（Ⅰ）求数列 ${a_{n}}$ 的通项公式；

（Ⅱ）令 $c_{n} = \frac{4}{b_{n} \cdot b_{n + 1}} + a_{n}$ ，求数列 ${c_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
18. 已知四棱锥中 $P - A B C D$ ，底面 $A B C D$ 为菱形， $∠ A B C = 60 °$ ， $P A ⊥$ 平面 $A B C D$ ， $E$ 、 $M$ 分别是 $B C$ 、 $P D$ 上的中点，直线 $E M$ 与平面 $P A D$ 所成角的正弦值为 $\frac{\sqrt{15}}{5}$ ，点 $F$ 在 $P C$ 上移动.

（Ⅰ）证明：无论点 $F$ 在 $P C$ 上如何移动，都有平面 $A E F ⊥$ 平面 $P A D$ ；

（Ⅱ）求点 $F$ 恰为 $P C$ 的中点时，二面角 $C - A F - E$ 的余弦值.

查看试题解析

19. 2012年12月18日，作为全国首批开展空气质量新标准监测的74个城市之一，郑州市正式发布

P M 2.5

数据.资料表明，近几年来，郑州市雾霾治理取得了很大成效，空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数（

A Q I

），其中在轻度污染区、中度污染区、重度污染区分别设有2，5，2个监测站点，以9个站点测得的

A Q I

的平均值为依据，播报我市的空气质量.

（Ⅰ）若某日播报的 $A Q I$ 为118，已知轻度污染区 $A Q I$ 的平均值为74，中度污染区 $A Q I$ 的平均值为114，求重度污染区 $A Q I$ 的平均值；

（Ⅱ）如图是2018年11月的30天中 $A Q I$ 的分布，11月份仅有一天 $A Q I$ 在 $[170 ， 180)$ 内.

组数	分组	天数
第一组	$[50 ， 80)$	3
第二组	$[80 ， 110)$	4
第三组	$[110 ， 140)$	4
第四组	$[140 ， 170)$	6
第五组	$[170 ， 200)$	5
第六组	$[200 ， 230)$	4
第七组	$[230.260)$	3
第八组	$[260 ， 290)$	1

①郑州市某中学利用每周日的时间进行社会实践活动，以公布的 $A Q I$ 为标准，如果 $A Q I$ 小于180，则去进行社会实践活动.以统计数据中的频率为概率，求该校周日进行社会实践活动的概率；

②在“创建文明城市”活动中，验收小组把郑州市的空气质量作为一个评价指标，从当月的空气质量监测数据中抽取3天的数据进行评价，设抽取到 $A Q I$ 不小于180的天数为 $X$ ，求 $X$ 的分布列及数学期望.

查看试题解析

20. 设 $M$ 点为圆 $C ： x^{2} + y^{2} = 4$ 上的动点，点 $M$ 在 $x$ 轴上的投影为 $N$ ，动点 $P$ 满足 $2 \overset{⇀}{P N} = \sqrt{3} \overset{⇀}{M N}$ ，动点 $P$ 的轨迹为 $E$ .
（Ⅰ）求 $E$ 的方程；

（Ⅱ）设 $E$ 的左顶点为 $D$ ，若直线 $l ： y = k x + m$ 与曲线 $E$ 交于两点 $A$ ， $B$ （ $A$ ， $B$ 不是左右顶点），且满足 $| \overset{⇀}{D A} + \overset{⇀}{D B} | = | \overset{⇀}{D A} - \overset{⇀}{D B} |$ ，求证：直线 $l$ 恒过定点，并求出该定点的坐标.

查看试题解析
21. 已知函数 $f (x) = x^{2} - 8 x + a ln x (a \in R)$ ．
$($ Ⅰ $)$ 当 $x = 1$ 时， $f (x)$ 取得极值，求 $a$ 的值并判断 $x = 1$ 是极大值点还是极小值点；

$($ Ⅱ $)$ 当函数 $f (x)$ 有两个极值点 $x_{1}$ ， $x_{2} (x_{1} < x_{2})$ ，且 $x_{1} \neq 1$ 时，总有 $\frac{a ln x_{1}}{1 - x_{1}} > t (4 + 3 x_{1} - x_{1}^{2})$ 成立，求 $t$ 的取值范围．

查看试题解析
22. 已知曲线 $C_{1} ： x^{2} + {(y - 3)}^{2} = 9$ ， $A$ 是曲线 $C_{1}$ 上的动点，以坐标原点 $O$ 为极点， $x$ 轴的正半轴为极轴建立极坐标系，以极点 $O$ 为中心，将点 $A$ 绕点 $O$ 逆时针旋转 $90 °$ 得到点 $B$ ，设点 $B$ 的轨迹方程为曲线 $C_{2}$ .
（Ⅰ）求曲线 $C_{1}$ ， $C_{2}$ 的极坐标方程；

（Ⅱ）射线 $θ = \frac{5 π}{6} (ρ > 0)$ 与曲线 $C_{1}$ ， $C_{2}$ 分别交于 $P$ ， $Q$ 两点，定点 $M (- 4 ， 0)$ ，求 $Δ M P Q$ 的面积.

查看试题解析
23. 已知函数 $f (x) = | 3 x - 2 a | + | 2 x - 2 | (a \in R)$ ．
$($ Ⅰ $)$ 当 $a = \frac{1}{2}$ 时，解不等式 $f (x) > 6$ ；

$($ Ⅱ $)$ 若对任意 $x_{0} \in R$ ，不等式 $f (x_{0}) + 3 x_{0} > 4 + | 2 x_{0} - 2 |$ 都成立，求 $a$ 的取值范围．

查看试题解析