河南省濮阳市2019届高三下学期文数摸底考试试卷

试卷更新日期：2019-04-29 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 2 ， - 1 ， 0 ， 1 ， 2}$ ，集合 $B = {x | (x - 1) (x + 2) < 0},$ 则 $A \cap B =$ （）

A、 ${- 1, 0}$ B、 ${0, 1}$ C、 ${- 1, 0, 1}$ D、 ${0, 1, 2}$

查看试题解析
2. 设i是虚数单位，若复数 $a - \frac{17}{4 - i} (a \in R)$ 是纯虚数，则实数a的值为（）

A、 $- 4$ B、 $- 1$ C、4 D、1

查看试题解析
3. 根据如表数据，得到的回归方程为 $\hat{y} = \hat{b} x + 9$ ，则 $\hat{b} = ($ 　　 $)$

x

4

5

6

7

8

y

5

4

3

2

1

A、2 B、1 C、0 D、 $- 1$

查看试题解析
4. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右顶点分别为A₁ ， A₂ ，且以线段A₁A₂为直径的圆与直线 $b x - a y + 2 a b = 0$ 相切，则C的离心率为（）

A、 $\frac{\sqrt{6}}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{1}{3}$

查看试题解析
5. 函数 $y = x^{3}$ 的图象在原点处的切线方程为（）

A、 $y = x$ B、 $x = 0$ C、 $y = 0$ D、不存在

查看试题解析
6. 执行右边的程序框图，若输出的S是127，则条件①可以为（）．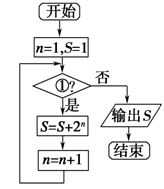

A、n≤5 B、n≤6 C、n≤7 D、n≤8

查看试题解析
7. 已知向量 $\vec{a}$ ， $\vec{b}$ 的夹角为 $\frac{2 π}{3}$ ，且 $\vec{a} = (3, - 4)$ ， $| \vec{b} | = 2$ ，则 $| 2 \vec{a} + \vec{b} | =$ （）

A、 $2 \sqrt{3}$ B、2 C、 $2 \sqrt{21}$ D、 $84$

查看试题解析
8. 如果函数 $f (x) = cos (ω x + \frac{π}{4})$ $(ω > 0)$ 的相邻两个零点之间的距离为 $\frac{π}{6}$ ，则 $ω$ 的值为（）

A、3 B、6 C、12 D、24

查看试题解析
9. 如图是一个多面体三视图，它们都是斜边长为的等腰，则这个多面体最长一条棱长为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $2 \sqrt{3}$ D、 $3 \sqrt{2}$

查看试题解析
10. 已知数列{a_n}的通项公式a_n＝26－2n，要使此数列的前n项和S_n最大，则n的值为（）

A、12 B、13 C、12或13 D、14

查看试题解析
11. 已知函数 $f (x)$ 满足条件：当 $x > 0$ 时， $f (x) + \frac{1}{2} x f^{'} (x) > 1$ ，则下列不等式正确的是（）

A、 $f (1) + 3 > 4 f (2)$ B、 $f (2) + 3 > 4 f (4)$ C、 $f (1) + 8 < 9 f (3)$ D、 $f (2) + 4 < 3 f (4)$

查看试题解析
12. 如图， $A B C D - A_{1} B_{1} C_{1} D_{1}$ 为正方体，下面结论错误的是（　　）

A、 $B D / /$ 平面 $C B_{1} D_{1}$ B、 $A C_{1} ⊥ B D$ C、 $A C_{1} ⊥$ 平面 $C B_{1} D_{1}$ D、异面直线 $A D$ 与 $C B_{1}$ 所成的角为 $60 °$

查看试题解析

二、填空题

13. 已知 $f (x) = {\begin{cases} 2^{x}, (x \leq 1) \\ lg (x - 1), (x > 1) \end{cases}$ ，则 $f (f (1)) =$ ．

查看试题解析
14. 若函数 $y = {log}_{2} x$ 的图像上存在点 $(x ， y)$ ，满足约束条件 ${\begin{matrix} x + y - 3 \leq 0 \\ 2 x - y + 2 \geq 0 \\ y \geq m \end{matrix}$ ，则实数 $m$ 的最大值为．

查看试题解析
15. 在 $Δ A B C$ 中，内角 $A, B, C$ 所对的边分别为 $a, b, c$ ,已知 $(a + b - c) (a + b + c) = 3 a b$ ，且 $c = 4$ ，则 $Δ A B C$ 面积的最大值为．

查看试题解析
16. 平面内与两定点 $A_{1} (0, - a)$ ， $A_{2} (0, a)$ $(a > 0)$ 连线的斜率之积等于非零常数 $m$ 的点的轨迹，加上 $A_{1}$ 、 $A_{2}$ 两点所成的曲线 $C$ 可以是圆、椭圆或双曲线.给出以下四个结论：
①当 $m = - 1$ 时，曲线 $C$ 是一个圆；②当 $m = - 2$ 时，曲线 $C$ 的离心率为 $\frac{\sqrt{2}}{2}$ ；

③当 $m = 2$ 时，曲线 $C$ 的渐近线方程为 $y = \pm \frac{\sqrt{2}}{2} x$ ；

④当 $m \in (- \infty, - 1) \cup (0, + \infty)$ 时，曲线 $C$ 的焦点坐标分别为 $(0, - a \sqrt{1 + \frac{1}{m}})$ 和 $(0, a \sqrt{1 + \frac{1}{m}})$ .其中全部正确结论的序号为.

查看试题解析

三、解答题

17. 在数列 ${a_{n}}$ 和等比数列 ${b_{n}}$ 中， $a_{1} = 0$ ， $a_{3} = 2$ ， $b_{n} = 2^{a_{n} + 1} (n \in N^{*})$ ．
$($ Ⅰ $)$ 求数列 ${b_{n}}$ 及 ${a_{n}}$ 的通项公式；

$($ Ⅱ $)$ 若 $c_{n} = a_{n} \cdot b_{n}$ ，求数列 ${c_{n}}$ 的前n项和 $S_{n}$ ．

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是平行四边形， $∠ B C D = 120 °$ ，侧面 $P A B ⊥$ 底面 $A B C D$ ， $∠ B A P = 90 °$ ， $A B = A C = P A = 2$ .

(1)、求证：面 $P B D ⊥$ 面 $P A C$ ；

(2)、过 $A C$ 的平面交 $P D$ 于点 $M$ ，若平面 $A M C$ 把四面体 $P - A C D$ 分成体积相等的两部分，求三棱锥 $M - P A B$ 的体积.

查看试题解析

19. 某单位从一所学校招收某类特殊人才．对

20

位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试，其测试结果如下表：

逻辑思维能力运动协调能力	一般	良好	优秀
一般	$2$	$2$	$1$
良好	$4$	$b$	$1$
优秀	$1$	$3$	$a$

例如表中运动协调能力良好且逻辑思维能力一般的学生是 $4$ 人．由于部分数据丢失，只知道从这 $20$ 位参加测试的学生中随机抽取一位，抽到逻辑思维能力优秀的学生的概率为 $\frac{1}{5}$ ．

(1)、求

a

，

b

的值；

(2)、从运动协调能力为优秀的学生中任意抽取

2

位，求其中至少有一位逻辑思维能力优秀的学生的概率．

查看试题解析

20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的一个焦点与上下顶点构成直角三角形，以椭圆C的长轴长为直径的圆与直线 $x + y - 2 = 0$ 相切．
$($ 1 $)$ 求椭圆C的标准方程；

查看试题解析
21. 已知函数 $f (x) = x^{2} - 2 (a + 1) x + 2 alnx (a > 0)$ ．

(1)、求 $f (x)$ 的单调区间；

(2)、若 $f (x) \leq 0$ 在区间 $[1 ， e]$ 上恒成立，求实数a的取值范围．

查看试题解析
22. 选修4-4：坐标系与参数方程
极坐标系的极点为直角坐标系 $x O y$ 的原点，极轴为 $x$ 轴的正半轴，两种坐标系中的长度单位相同，已知曲线 $C$ 的极坐标方程为 $ρ = 2 (cos θ + sin θ)$ .

(1)、求 $C$ 的直角坐标方程；

(2)、直线 $l : {\begin{matrix} x = \frac{1}{2} t \\ y = 1 + \frac{\sqrt{3}}{2} t \end{matrix}$ （ $t$ 为参数）与曲线 $C$ 交于 $A, B$ 两点，与 $y$ 轴交于 $E$ ，求 $| E A | + | E B |$ .

查看试题解析
23. 已知函数 $f (x) = | 2 x + 1 |$ ， $g (x) = | x | + a$
$($ 1 $)$ 当 $a = 0$ 时，解不等式 $f (x) \geq g (x)$ ；

查看试题解析