2018-2019学年初中数学北师大版七年级下册6.2频率的稳定性 同步练习
试卷更新日期：2019-04-29 类型：同步测试
一、单选题
-
1. 做抛掷同一枚啤酒瓶盖的重复试验，经过统计得“凸面朝上”的频率约为0.44，则可以估计抛掷这枚啤酒瓶盖出现“凸面朝上”的概率约为（ ）A、22% B、44% C、50% D、56%2. 布袋里有50个形状完全相同的小球，小红随机摸出一个球，记下颜色后放回摇匀，重复以上操作300次，发现摸到白色的球有61次，则布袋中白球的个数最有可能是（ ）A、5个 B、10个 C、15个 D、20个3. 在一个不透明的布袋中装有40个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.30左右，则布袋中黄球可能有（ ）A、12个 B、14个 C、18个 D、28个4. 在一次比赛前，教练预言说：“这场比赛我们队有60%的机会获胜”，则下列说法中与“有60%的机会获胜”的意思接近的是（ ）
A、他这个队赢的可能性较大 B、若这两个队打10场，他这个队会赢6场 C、若这两个队打100场，他这个队会赢60场 D、他这个队必赢5. 小张承包了一片荒山，他想把这片荒山改造成一个苹果园，现在有一种苹果树苗，它的成活率如下表所示：
移植棵数（n）
成活数(m)
成活率(m/n)
移植棵数（n）
成活数(m)
成活率(m/n)
50
47
0.940
1500
1335
0.890
270
235
0.870
3500
3203
0.915
400
369
0.923
7000
6335
0.905
750
662
0.883
14000
12628
0.902
下面有四个推断：
①当移植的树数是1 500时，表格记录成活数是1 335，所以这种树苗成活的概率是0.890；②随着移植棵数的增加，树苗成活的频率总在0.900附近摆动，显示出一定的稳定性，可以估计树苗成活的概率是0.900；③若小张移植10 000棵这种树苗，则可能成活9 000棵；④若小张移植20 000棵这种树苗，则一定成活18 000棵.其中合理的是（ ）
A、①③ B、①④ C、②③ D、②④6. 下列说法中错误的是（ ）A、概率很小的事件不可能发生 B、不可能事件发生的概率为0 C、随机事件发生的概率大于或等于0且小于或等于1 D、必然事件发生的概率为17. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下折线统计图，则符合这一结果的实验最有可能的是（ ）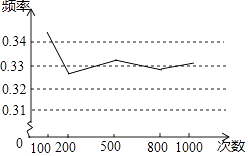
A、袋中装有大小和质地都相同的3个红球和2个黄球，从中随机取一个，取到红球 B、掷一枚质地均匀的正六面体骰子，向上的面的点数是偶数 C、先后两次掷一枚质地均匀的硬币，两次都出现反面 D、先后两次掷一枚质地均匀的正六面体骰子，两次向上的面的点数之和是7或超过98. 某水果超市为了吸引顾客来店购物，设立了一个如图所示的可以自由转动的转盘，开展有奖购物活动．顾客购买商品满200元就能获得一次转动转盘的机会，当转盘停止时，指针落在“一袋苹果”的区域就可以获得“一袋苹果”的奖品；指针落在“一盒樱桃”的区域就可以获得“一盒樱桃”的奖品．下表是该活动的一组统计数据：转动转盘的次数n
100
150
200
500
800
1000
落在“一袋苹果”区域的次数m
68
108
140
355
560
690
落在“一袋苹果”区域的频率
0.68
0.72
0.70
0.71
0.70
0.69
下列说法不正确的是（ ）
A、当n很大时，估计指针落在“一袋苹果”区域的频率大约是0.70 B、假如你去转动转盘一次，获得“一袋苹果”的概率大约是0.70 C、如果转动转盘2 000次，指针落在“一盒樱桃”区域的次数大约有600次 D、转动转盘10次，一定有3次获得“一盒樱桃”9. 某小组做“用频率估计概率”的实验时，绘出的某一结果出现的频率折线图，则符合这一结果的实验可能是（ ）
A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现3点朝上 C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球10. 2012﹣2013NBA整个常规赛季中，科比罚球投篮的命中率大约是83.3%，下列说法错误的是（ ）
A、 科比罚球投篮2次，一定全部命中 B、科比罚球投篮2次，不一定全部命中 C、科比罚球投篮1次，命中的可能性较大 D、科比罚球投篮1次，不命中的可能性较小二、填空题
-
11. 某射手在相同条件下进行射击训练，结果如下：
射击次数n
10
20
40
50
100
200
500
1000
击中靶心的频数m
8
19
37
45
89
181
449
901
击中靶心的频率
0.900
0.950
0.925
0.900
0.890
0.905
0.898
0.901
该射手击中靶心的概率的估计值是（明确到0.01）．
12. 在一个不透明的盒子中装有n个规格相同的乒乓球，其中有2个黄色球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复试验后发现，摸到黄色球的频率稳定于0.2，那么可以推算出n大约是 ．13. 下图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果. 随着实验次数的增加，“钉尖向上”的频率总在一常数附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是
14. 一个圆形转盘的半径为2cm，现将转盘分成若干个扇形，并分别相间涂上红、黄两种颜色．转盘转动10 000次，指针指向红色部分有2 500次．请问指针指向红色的概率的估计值是 ， 转盘上黄色部分的面积大约是 ．
15. 林业部门要考察某种幼树在一定条件下的移植成活率，如图是这种幼树在移植过程中幼树成活率的统计图：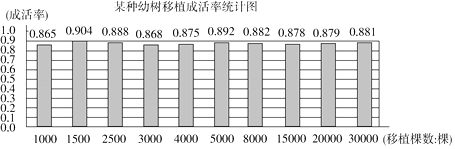
估计该种幼树在此条件下移植成活的概率为（结果精确到0.01）．
三、解答题
-
16. 一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字3，4，5，x.甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复试验.试验数据如下表.
摸球
总次数
10
20
30
60
90
120
180
240
330
450
“和为8”出
现的次数
2
10
13
24
30
37
58
82
110
150
“和为8”出
现的频率
0.20
0.50
0.43
0.40
0.33
0.31
0.32
0.34
0.33
0.33
(1)、10次试验“和为8”出现的频率是 ， 20次试验“和为8”出现的频率是 ， 450次试验“和为8”出现的频率是；(2)、如果试验继续进行下去，根据上表数据，估计出现“和为8”的概率是.17. 某商场设立了一个可以自由转动的转盘(如图)，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品，下表是活动进行中的一组统计数据：
(1)、计算并完成表格：转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”的次数m
68
111
136
345
546
701
落在“铅笔”的频率
(2)、假如你去转动该转盘一次，你获得铅笔的概率约是多少？
18. 小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）试验，她们共做了60次试验，试验的结果如下：朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)、计算“3点朝上”的频率和“5点朝上”的频率.
(2)、小颖说：“根据上述试验，一次试验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗？为什么？
19. 在一个不透明的盒子里装有颜色不同的黑、白两种球共40个，小颖做摸球试验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是“摸到白色球”的频率折线统计图.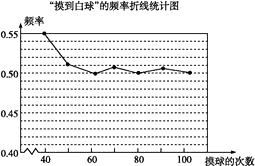
(1)、请估计：当n足够大时，摸到白球的频率将会稳定在(精确到0.01)，假如你摸一次，你摸到白球的概率为；
(2)、试估算盒子里白、黑两种颜色的球各有多少个?
(3)、在(2)条件下如果要使摸到白球的概率为 ，需要往盒子里再放入多少个白球?
20. 下表记录了一名球员在罚球线上投篮的结果，投篮次数（n）
50
100
150
209
250
300
350
投中次数（m）
28
60
78
104
123
152
175
投中频率（n/m）
0.56
0.60
0.49
（1）计算并填写表中的投中频率（精确到0.01）；
（2）这名球员投篮一次，投中的概率约是多少（精确到0.1）？
21. 下面给大家介绍密码破译的知识：密码破译本质上是一个寻找偶然事情规律的一种游戏．为了简明，我们以英语例子加以说明．
如果要传递的消息是用英语写的，你可以随意地用两个数字来代替英语中的一个字母，比如为叙述方便，用00，01，02，…25来代替26个英文字母，而每个单词之间用26隔开．当接到这样编排密码时首先要对所有的数码在密码中出现的次数进行统计，算出每个数码出现的频率．再逐步分析出每个数码代表的是哪个字母，弄清了这个问题，密码也就能破译出来了．假如你收到的密码中有一段是：
070015152426130422262404001726191426241420
你能破译出这段密码吗？