广西桂林市、贺州市、崇左市2019届高三下学期文数3月联合调研考试试卷
试卷更新日期:2019-04-29 类型:高考模拟
一、单选题
-
1. 设集合 , ,则 ( )A、 B、 C、 D、2. 已知复数 ,则 ( )A、4 B、3 C、5 D、23. , , ,则 的大小关系为( )A、 B、 C、 D、4. 设 为等差数列 的前 项和,若 , ,则 的公差为( )A、1 B、3 C、6 D、25. 已知 ,则 ( )A、 B、 C、 D、6. 某市气象部门根据2018年各月的每天最高气温平均值与最低气温平均值(单位: )数据,绘制如下折线图:

那么,下列叙述错误的是( )
A、各月最高气温平均值与最低气温平均值总体呈正相关 B、全年中,2月份的最高气温平均值与最低气温平均值的差值最大 C、全年中各月最低气温平均值不高于 的月份有5个 D、从2018年7月至12月该市每天最高气温平均值与最低气温平均值呈下降趋势7. 某几何体的三视图如图所示,则该几何体的体积是( ) A、8 B、6 C、4 D、28. 函数 的大致图像为( )A、
A、8 B、6 C、4 D、28. 函数 的大致图像为( )A、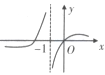 B、
B、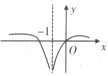 C、
C、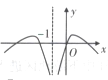 D、
D、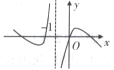 9. 已知圆 截直线 所得弦的长度为4,则实数 ( )A、-2 B、-4 C、-6 D、-810. 已知函数 ,若 ,且 ,则函数 取得最大值时 的可能值为( )A、 B、 C、 D、11. 已知 为椭圆 上三个不同的点, 为坐标原点,若 ,则 的面积为( )A、 B、 C、 D、
9. 已知圆 截直线 所得弦的长度为4,则实数 ( )A、-2 B、-4 C、-6 D、-810. 已知函数 ,若 ,且 ,则函数 取得最大值时 的可能值为( )A、 B、 C、 D、11. 已知 为椭圆 上三个不同的点, 为坐标原点,若 ,则 的面积为( )A、 B、 C、 D、二、填空题
-
12. 已知 , ,则向量 .13. 已知 满足 则 的最大值为 .14. 在三棱锥 中, , , , ,则三棱锥 外接球的体积的最小值为 .15. 已知函数 ,函数 有三个不同的零点 , , ,则 的取值范围是 .
三、解答题
-
16. 的三个内角 所对的边分别为 ,已知 .(1)、求 的值;(2)、若 ,求 .17. 某校为了调查高三男生和女生周日学习用时情况,随机抽取了高三男生和女生各40人,对他们的周日学习时间进行了统计,分别得到了高三男生的学习时间(单位:小时)的频数分布表和女生的学习时间的频率分布直方图.)(学习时间均在 内)
男生周日学习时间频数表
学习时间
频数
8
10
7
9
4
2
女生周日学习时间频率分布直方图
 (1)、根据调查情况,该校高三年级周日学习用时较长的是男生还是女生?请说明理由;(2)、从被抽到的80名高三学生中周日学习用时在 内的学生中抽取2人,求恰巧抽到1男1女的概率.18. 已知三棱柱 中, , , , .
(1)、根据调查情况,该校高三年级周日学习用时较长的是男生还是女生?请说明理由;(2)、从被抽到的80名高三学生中周日学习用时在 内的学生中抽取2人,求恰巧抽到1男1女的概率.18. 已知三棱柱 中, , , , . (1)、求证:平面 平面 ;(2)、若 , 为线段 的中点,求三棱锥 的体积.19. 已知抛物线 ,过点 的直线 交抛物线于 、 两点,设 为坐标原点,点 .(1)、求 的值;(2)、若 , , 的面积成等比数列,求直线 的方程.
(1)、求证:平面 平面 ;(2)、若 , 为线段 的中点,求三棱锥 的体积.19. 已知抛物线 ,过点 的直线 交抛物线于 、 两点,设 为坐标原点,点 .(1)、求 的值;(2)、若 , , 的面积成等比数列,求直线 的方程.