安徽省淮南市2019届高三文数第一次模拟考试试卷

试卷更新日期：2019-04-29 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $P = {x | - 1 < x < 1}$ ， $Q = {x | - 2 < x < \frac{1}{2}}$ ，则 $P \cup^{} Q = ($ 　　 $)$

A、 $(- 1 ， \frac{1}{2})$ B、 $(- 2 ， 1)$ C、 $(\frac{1}{2} ， 1)$ D、 $(- 2 ， - 1)$

查看试题解析
2. $| 1 + 2 i | = ($ 　　 $)$

A、 $\sqrt{3}$ B、 $\sqrt{7}$ C、 $\sqrt{5}$ D、3

查看试题解析
3. 函数 $f (x) = x^{2} (e^{x} - e^{- x})$ 的大致图象为 $($ 　　 $)$

A、 B、 C、 D、

查看试题解析
4. 某三棱锥的三视图如图所示，其侧（左）视图为直角三角形，则该三棱锥外接球的表面积为（）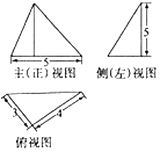

A、50π B、50 $\sqrt{2}$ π C、40π D、40 $\sqrt{2}$ π

查看试题解析
5. 已知锐角△ABC的内角A，B，C的对边分别为a，b，c，23cos²A+cos 2A=0，a=7，c=6，则b等于（）

A、10 B、9 C、8 D、5

查看试题解析
6. 在平行四边形 $A B C D$ 中，已知 $A B = 4$ ， $A D = 3$ ， $\vec{C P} = 3 \vec{P D}$ ， $\vec{A P} \cdot \vec{B P} = 2$ ，则 $\vec{A B} \cdot \vec{A D}$ 的值是 $($ 　　 $)$

A、4 B、6 C、8 D、10

查看试题解析
7. 如图为我国数学家赵爽约3世纪初在为《周髀算经》作注时验证勾股定理的示意图，它是由4个全等的直角三角形与中间的小正方形拼成的一个大正方形，现向大正方形内丢一粒黄豆，当每个直角三角形的两直角边之比都是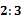时，则该黄豆落入小正方形内的概率为 $($ 　　 $)$

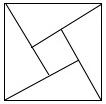A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{2}{13}$ D、 $\frac{1}{13}$

查看试题解析
8. 某圆锥的侧面展开图是面积为 $3 π$ ，圆心角为 $\frac{2 π}{3}$ 的扇形，则该圆锥的母线与底面所成的角的余弦值为 $($ 　　 $)$

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
9. 已知奇函数 $f (x)$ 满足 $f (x) = f (x + 4)$ ，当 $x \in (0 ， 1)$ 时， $f (x) = 4^{x}$ ，则 $f ({log}_{4} 184) = ($ 　　 $)$

A、 $- \frac{32}{23}$ B、 $\frac{23}{32}$ C、 $\frac{3}{4}$ D、 $- \frac{3}{8}$

查看试题解析
10. 已知点 $P$ 是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 右支上一点， $F_{1}$ 、 $F_{2}$ 分别是双曲线的左、右焦点， $M$ 为 $△ P F_{1} F_{2}$ 的内心，若 $S_{△ M P F_{1}} = S_{△ M P F_{2}} + \frac{1}{2} S_{△ M F_{1} F_{2}}$ 成立，则双曲线的离心率为 $($ 　　 $)$

A、4 B、 $\frac{5}{2}$ C、2 D、 $\frac{5}{3}$

查看试题解析
11. 如图是函数 $y = sin (ω x + φ) (ω > 0 ， 0 < φ < \frac{π}{2})$ 在区间 $[- \frac{π}{6} ， \frac{5 π}{6}]$ 上的图象，将该图象向右平移 $| m | (m < 0)$ 个单位后，所得图象关于直线 $x = \frac{π}{4}$ 对称，则 $m$ 的最大值为 $($ 　　 $)$

A、 $- \frac{π}{12}$ B、 $- \frac{π}{6}$ C、 $- \frac{π}{4}$ D、 $- \frac{π}{3}$

查看试题解析
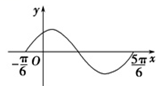12. 在平面直角坐标系中，设点 $p (x ， y)$ ，定义 $[O P] = | x | + | y |$ ，其中 $O$ 为坐标原点，对于下列结论：
$(1)$ 符合 $[O P] = 2$ 的点 $p$ 的轨迹围成的图形面积为8；

$(2)$ 设点 $p$ 是直线： $\sqrt{3} x + 2 y - 2 = 0$ 上任意一点，则 ${[O P]}_{m i n} = 1$ ；

$(3)$ 设点 $p$ 是直线： $y = k x + 1 (k \in R)$ 上任意一点，则使得“ $[O P]$ 最小的点 $p$ 有无数个”的必要条件是 $k = 1$ ；

$(4)$ 设点 $p$ 是圆 $x^{2} + y^{2} = 2$ 上任意一点，则 ${[O P]}_{m a x} = 2$ ．

其中正确的结论序号为 $($ 　　 $)$

A、 $(1) (2) (3)$ B、 $(1) (3) (4)$ C、 $(2) (3) (4)$ D、 $(1) (2) (4)$

查看试题解析

二、解答题

13. 已知直线 $l$ 过点 $P (1, 0)$ ，且倾斜角为 $α$ ，以坐标原点为极点， $x$ 轴的正半轴为极轴建立坐标系，圆 $C$ 的极坐标方程为 $ρ = 4 cos θ$ ．

(1)、求圆 $C$ 的直角坐标系方程及直线 $l$ 的参数方程；

(2)、若直线 $l$ 与圆 $C$ 交于 $A, B$ 两点，求 $\frac{1}{| P A |} + \frac{1}{| P B |}$ 的最大值和最小值．

查看试题解析