浙江省2019届高考数学模拟卷(一)
试卷更新日期:2019-04-29 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 若复数 满足 ,在复数 的虚部为( )A、 B、1 C、-1 D、3. 已知 是双曲线 渐近线上的点,则双曲线 的离心率是( )A、2 B、 C、 D、4. 设 , 满足约束条件 ,则 的最小值是( )A、1 B、 C、 D、5. 已知圆 .设条件 ,条件 圆 上至多有 个点到直线 的距离为 ,则 是 的A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 已知函数 的图像相邻的两个对称中心之间的距离为 ,若将函数 的图像向左平移 后得到偶函数 的图像,则函数 的一个单调递减区间为( )A、 B、 C、 D、7. 如图,已知函数 的图像关于坐标原点对称,则函数 的解析式可能是( )
 A、 B、 C、 D、8. 设函数 是定义在 上的可导函数,其导函数为 ,且有 ,则不等式 的解集为( )A、 B、 C、 D、9. 定义域为 的偶函数 满足对 ,有 ,且当 时, ,若函数 至少有6个零点,则 的取值范围是( )
A、 B、 C、 D、8. 设函数 是定义在 上的可导函数,其导函数为 ,且有 ,则不等式 的解集为( )A、 B、 C、 D、9. 定义域为 的偶函数 满足对 ,有 ,且当 时, ,若函数 至少有6个零点,则 的取值范围是( )
A、 B、 C、 D、10. 如图,在 中, , , 为 上一点,且满足 ,若 的面积为 ,则 的最小值为( )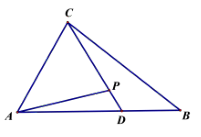 A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题
-
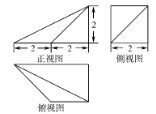
11. 已知函数 则 , 的最小值为 .12. 已知一个袋子中装有4个红球和2个白球,假设每一个球被摸到的可能性是相等的,若从袋子中摸出3个球,记摸到的白球的个数为 ,则 的概率是;随机变量 期望是.13. 设 ,则 , ( 的值为 .14. 某几何体的三视图如图所示,则该几何体的表面积为;体积为.
 |15. 某书店有11种杂志,2元1本的8种,1元1本的3种,小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是(用数字作答).16. 已知圆 : ( 为正实数)上任意一点关于直线 : 的对称点都在圆 上,则 的最小值为 .17. 四棱锥 中, 平面ABCD, , ,BC//AD,已知Q是四边形ABCD内部一点,且二面角 的平面角大小为 ,若动点Q的轨迹将ABCD分成面积为 的两部分,则 = .
|15. 某书店有11种杂志,2元1本的8种,1元1本的3种,小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是(用数字作答).16. 已知圆 : ( 为正实数)上任意一点关于直线 : 的对称点都在圆 上,则 的最小值为 .17. 四棱锥 中, 平面ABCD, , ,BC//AD,已知Q是四边形ABCD内部一点,且二面角 的平面角大小为 ,若动点Q的轨迹将ABCD分成面积为 的两部分,则 = .三、解答题
-
18. 已知函数 .(1)、求该函数图象的对称轴;(2)、在 中,角 所对的边分别为 ,且满足 ,求 的取值范围.19. 四棱锥 中, 平面 , 为 的中点, 为菱形, , , 、 分别是线段 、 的中点.

(Ⅰ)求证: 平面 ;
(Ⅱ)求二面角 的正切值.
