2018-2019学年初中数学北师大版七年级下册5.3简单的轴对称图形 同步练习
试卷更新日期：2019-04-28 类型：同步测试
一、单选题
-
1. 如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD＝2，则点P到边OA的距离是（ ）
A、1 B、2 C、 D、42. 下列图形中，对称轴的条数最多的是（ ）A、长方形 B、正方形 C、等腰三角形 D、线段3. 如图，在△ABE中，AE的垂直平分线MN交BE于点C，∠E=30°，且AB=CE，则∠BAE的度数是（ ）
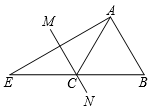A、80° B、85° C、90° D、105°4. 如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，DE=3，BD=2CD， 则BC=（ ）
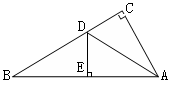A、7 B、8 C、9 D、105. 如果等腰三角形有一个内角为70°，则其底角的度数是（ ）．A、55° B、70° C、55°或70° D、不确定6. 用一条长为16cm的细绳围成一个等腰三角形，若其中有一边的长为4cm，则该等腰三角形的腰长为（ ）A、4cm B、6cm C、4cm或6cm D、4cm或8cm7. 如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（ ）
A、4 B、3 C、2 D、18. 如图，AB∥CD，AP，CP分别平分∠BAC和∠ACD，PE⊥AC于点E，且PE＝3cm，则AB与CD之间的距离为（ ）
A、3 cm B、6 cm C、9 cm D、无法确定9. 如图，在△ABC中，分别以点A和点B为圆心，大于 AB长为半径画弧，两弧分别相交于点M，N，作直线MN，交BC于点D，连结AD．若△ADC的周长为10，AB＝7，则△ABC的周长为（ ）
A、27 B、14 C、17 D、2010. 如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AEB为（ ）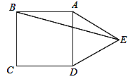
A、10° B、15° C、20° D、125°二、填空题
-
11. 如图，△ABC的AC边的垂直平分线DE交BC于点E，若BC=4，AB=3，则△ABE的周长为
12. 如图，在△ABC中，AD是∠BAC的平分线，DE⊥AB于点E， ，DE=2，AB=4，则AC的长是 ．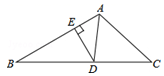
13. 如图，在△ABC中，分别以点A和点B为圆心，大于 AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB＝7，则△ABC的周长为 ．
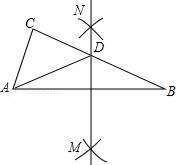14. 如图，在 中， ， ， 的垂直平分线 交 于点 ，则 ．
15. 等腰△ABC中，有一个角等于40°，则这个等腰三角形的顶角大小为 ．16. 如图，在△ABC中，AD是它的角平分线，若S△ABD：S△ACD＝3：2，则AB：AC＝ ．
三、解答题
-
17. 如图所示，在△ABC中，∠ABC=∠C，BD⊥AC交AC于D．
求证：∠DBC= ∠A．
18. 如图，△ABC中，AB=AC，∠A=50°，AB的垂直平分线DE分别交AC、AB于点D、E．求∠CBD的度数．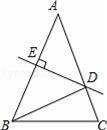
19. 如图，在△ABC中，∠ACB=90∘，D是BC延长线上一点，E是BD的垂直平分线与AB的交点，DE交AC于点F，求证：EA=EF.
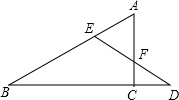20. 一个等腰三角形的一边长为6cm，周长为20cm，求其他两边的长．21. 如图，在等边△ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E(点E不与点A重合）．
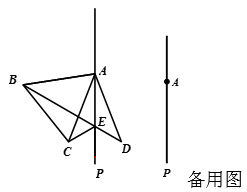(1)、若∠CAP=20°.①求∠AEB=°；
②连结CE，直接写出AE，BE，CE之间的数量关系 ．
(2)、若∠CAP= (0º< <120º).①∠AEB的度数是否发生变化，若发生变化，请求出∠AEB度数；
②AE，BE，CE之间的数量关系是否发生变化，并证明你的结论.
22. 已知：如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．
(1)、求证：AD=BE；(2)、拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，D点、E点关于直线CM对称，连接BE．探索线段CM、AE、BE之间有何数量关系，请说明理由.