2018-2019学年初中数学北师大版七年级下册5.2探索轴对称的性质 同步练习
试卷更新日期：2019-04-28 类型：同步测试
一、单选题
-
1. 如图所示，将长方形ABCD的一角沿AE折叠，若∠BAD′=40°，那么∠EAD′的度数为（ ）
A、20 B、25° C、40° D、50°2. 如图是经过轴对称变换后所得的图形，与原图形相比（ ）
A、形状没有改变，大小没有改变 B、形状没有改变，大小有改变 C、形状有改变，大小没有改变 D、形状有改变，大小有改变3. 如图，正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′，下列判断错误的是（ ）
A、AB=A′B′ B、BC∥B′C′ C、直线l⊥BB′ D、∠A′=120°4. 如图，将△ABC沿直线DE折叠后，使得点B与点A重合，已知AC=4cm，△ADC的周长为15cm，则BC的长为（ ）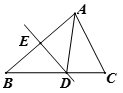
A、8cm B、11cm C、13cm D、19cm5. 把26个英文字母按规律分成5组，现在还有5个字母D、M、Q、X、Z，请你按原规律补上，其顺序依次为（ ）⑴F，R，P，J，L，G，（ ）
⑵H，I，O，（ ）
⑶N，S，（ ）
⑷B，C，K，E，（ ）
⑸V，A，T，Y，W，U，（ ）
A、Q，X，Z，M，D B、D，M，Q，Z，X C、Z，X，M，D，Q D、Q，X，Z，D，M6. 将一个矩形纸片按如图所示折叠，若∠1＝40°，则∠2的度数是（ ）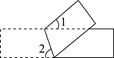
A、40° B、50° C、60° D、70°7. 如图，直线L是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站，向P，Q 两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（ ）A、
B、
C、
D、
8. 如图，△ABC和△A′B′C′关于直线L对称，下列结论中正确的有（ ）（1）△ABC≌△A′B′C′（2）∠BAC=∠B′A′C′（3）直线L垂直平分CC′（4）直线BC和B′C′的交点不一定在直线L上．
A、4个 B、3个 C、2个 D、1个9. 已知△ABC关于直线MN对称，则下列说法错误的是（ ）A、△ABC中必有一个顶点在直线MN上 B、△ABC中必有两个角相等 C、△ABC中，必有两条边相等 D、△ABC中必有有一个角等于60°二、填空题
-
10. 如图是一个风筝的图案，它是轴对称图形，量得∠B=20°，则∠E=°．
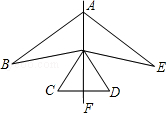11. 如图，点P关于OA，OB的对称点分别为C、D，连接CD，交OA于M，交OB于N，若CD=18cm，则△PMN的周长为cm．
12. 如图，Rt△AFC和Rt△AEB关于虚线成轴对称，现给出下列结论：①∠1=∠2；②△ANC≌△AMB；③CD=DN．其中正确的结论是 ． （填序号）
13. 如图是跳棋盘，其中格点上的黑色点为棋子，剩余的格点上没有棋子．我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内，沿着棋子对称跳行，跳行一次称为一步．已知点A为己方一枚棋子，欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最少步数为步．
14. 如图，P为△ABC内的一点，D，E，F分别是点P关于边AB，BC，CA所在直线的对称点，那么∠ADB+∠BEC+∠CFA=°.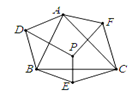
15. 如图，石头A和石头B相距80cm，且关于竹竿l对称，一只电动青蛙在距竹竿30cm，距石头A为60cm的P1处，按如图所示的顺序循环跳跃．青蛙跳跃25次后停下，此时它与石头A相距cm，与竹竿l相距cm．
三、解答题
-
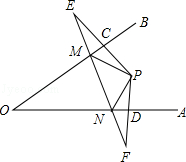
16. 如图，点P是∠AOB内一点，分别作出P点关于OA、OB的对称点E、F，连接EF交OA于M，交OB于N，EF=15，求△PMN的周长．
17. 如图，一个牧童在小河的南2km的A处牧马，而他正位于他的小屋B的西 km北3km处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？
18.
(1)、已知：如图，点M在锐角∠AOB的内部，在OA边上求作一点P，在OB边上求作一点Q，使得ΔPMQ的周长最小；
(2)、已知：如图，点M在锐角∠AOB的内部，在OB边上求作一点P，使得点P到点M的距离与点P到OA边的距离之和最小．
19. 数的计算中有一些有趣的对称形式，如：12×231=132×21；仿照上面的形式填空，并判断等式是否成立：(1)、12×462=×（），(2)、18×891=×（）．20. 如图，把△ABC沿DE折叠，使点A落在四边形BCDE内部的点A'处.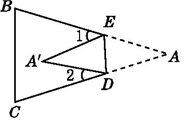
(1)、写出图中一对全等的三角形，并写出它们的所有对应角.(2)、设∠AED的度数为x，∠ADE的度数为y，那么∠1，∠2的度数分别是多少(用含有x或y的式子表示)?(3)、∠A与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律.21. 资料：小球沿直线撞击水平格档反弹时（不考虑垂直撞击），撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角．以图（1）为例，如果黑球 沿从 到 方向在 点处撞击 边后将沿从 到 方向反弹，根据反弹原则可知 ，即 ．如图（2）和（3）， 是一个长方形的弹子球台面，有黑白两球 和 ，小球沿直线撞击各边反弹时遵循资料中的反弹原则．（回答以下问题时将黑白两球均看作几何图形中的点，不考虑其半径大小）
(1)、探究（1）：黑球 沿直线撞击台边 哪一点时，可以使黑球 经台边 反弹一次后撞击到白球 ?请在图（2）中画出黑球 的路线图，标出撞击点，并简单证明所作路线是否符合反弹原则.(2)、探究（2）：黑球 沿直线撞击台边 哪一点时，可以使黑球 先撞击台边 反弹一次后，再撞击台边 反弹一次撞击到白球 ?请在图（3）中画出黑球 的路线图，标出黑球撞击 边的撞击点，简单说明作法，不用证明．