2018-2019学年初中数学浙教版八年级下册6.3反比例函数的应用 同步练习
试卷更新日期:2019-04-28 类型:同步测试
一、单选题
-
1. 在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )与体积 (单位: )满足函数关系式 ( 为常数, ),其图象如图所示,则 的值为()
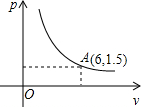
A、 B、
B、 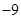 C、 4
D、
C、 4
D、 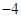 2. 一司机驾驶汽车从甲地去乙地,他以 千米/时的平均速度用了 小时到达目的地,当他按原路匀速返回时,汽车的速度 (千米/时)与时间 (小时)的函数关系为( )A、
2. 一司机驾驶汽车从甲地去乙地,他以 千米/时的平均速度用了 小时到达目的地,当他按原路匀速返回时,汽车的速度 (千米/时)与时间 (小时)的函数关系为( )A、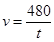 B、
B、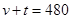 C、
C、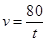 D、
D、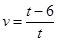 3. 小明乘车从南充到成都,行车的速度 和行车时间 之间的函数图象是( )
3. 小明乘车从南充到成都,行车的速度 和行车时间 之间的函数图象是( )
A、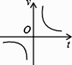 B、
B、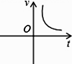 C、
C、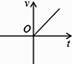 D、
D、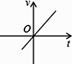 4. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
4. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )体积 x(mL) 100 80 60 40 20 压强 y(kPa) 60 75 100 150 300
A、 000x B、 000x C、 D、5. 已知水池的容量为50米3 , 每时灌水量为n米3 , 灌满水所需时间为t(时),那么t与n之间的函数关系式是( )A、t=50n B、t=50﹣n C、t= D、t=50+n6. 一个圆柱的侧面展开图是一个面积为10的矩形,这个圆柱的高为L与这个圆柱的底面半径r之间的函数关系为( )A、正比例函数 B、反比例函数 C、一次函数 D、二次函数7. 一张正方形的纸片,剪去两个一样的小矩形得到一个E”图案,如图所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( ) A、
A、 B、
B、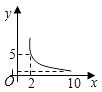 C、
C、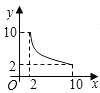 D、
D、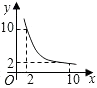 8. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为( )A、 B、 C、 D、y=9. 如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )
8. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为( )A、 B、 C、 D、y=9. 如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )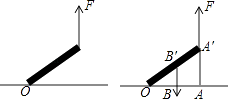 A、变大 B、变小 C、不变 D、无法判断10. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A、变大 B、变小 C、不变 D、无法判断10. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )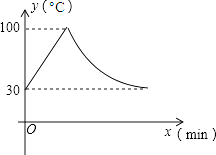 A、7:20 B、7:30 C、7:45 D、7:50
A、7:20 B、7:30 C、7:45 D、7:50二、填空题
-
11. 完成某项任务可获得500元报酬,考虑由 x人完成这项任务,试写出人均报酬 y(元)与人数 x(人)之间的函数关系式 .12. 如图所示蓄电池的电压为定值,使用该蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的电器的限制电流不超过12A,那么用电器可变电阻R应控制的范围是 .
 13. 长方体的体积为103 m3 , 底面积为S,高度为d,则S与d之间的函数关系式为 ;当S=500时,d=.14. 一定质量的氧气,它的密度 是它的体积 的反比例函数.当 时, ,则 与 的函数关系是 .
13. 长方体的体积为103 m3 , 底面积为S,高度为d,则S与d之间的函数关系式为 ;当S=500时,d=.14. 一定质量的氧气,它的密度 是它的体积 的反比例函数.当 时, ,则 与 的函数关系是 .
15. 有一面积为120的梯形,其上底是下底长的 ,若上底长为x,高为y,则y与x的函数关系式为 ;当高为10时,x=.
16. 在照明系统模拟控制电路实验中,研究人员发现光敏电阻值R(单位:Ω)与光照度E(单位:lx)之间成反比例函数关系,部分数据如下表所示,则光敏电阻值R与光照度E的函数表达式为 .光照度E/lx
0.5
1
1.5
2
2.5
3
光敏电阻阻值R/Ω
60
30
20
15
12
10
三、综合题
-
17. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:(1)、假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)、若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)、在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?18. 某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.(1)、求甲、乙两种品牌空调的进货价;(2)、该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.19. 小明对某市出租汽车的计费问题进行研究,他搜集了一些资料,部分信息如下:收费项目
收费标准
3公里以内收费
13元
基本单价
2.3元/公里
……
……
备注:出租车计价段里程精确到500米;出租汽车收费结算以元为单位,元以下四舍五入.
小明首先简化模型,从简单情形开始研究:①只考虑白天正常行驶(无低速和等候);②行驶路程3公里以上时,计价器每500米计价1次,且每1公里中前500米计价1.2元,后500米计价1.1元.
下面是小明的探究过程,请补充完整:
记一次运营出租车行驶的里程数为x(单位:公里),相应的实付车费为y(单位:元).
(1)、下表是y随x的变化情况行驶里程数x
0
0<x<3.5
3.5≤x<4
4≤x<4.5
4.5≤x<5
5≤x<5.5
…
实付车费y
0
13
14
15
…
(2)、在平面直角坐标系xOy中,画出当0<x<5.5时y随x变化的函数图象;(3)、一次运营行驶x公里(x>0)的平均单价记为w(单位:元/公里),其中w= .①当x=3,3.4和3.5时,平均单价依次为w1 , w2 , w3 , 则w1 , w2 , w3的大小关系是;(用“<”连接)
②若一次运营行驶x公里的平均单价w不大于行驶任意s(s≤x)公里的平均单价ws , 则称这次行驶的里程数为幸运里程数.请在上图中x轴上表示出3~4(不包括端点)之间的幸运里程数x的取值范围.
20. 为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题: (1)、药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范为;药物燃烧后,y关于x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?21. 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)、药物燃烧时,y关于x的函数关系式为 , 自变量x的取值范为;药物燃烧后,y关于x的函数关系式为 .(2)、研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过分钟后,员工才能回到办公室;(3)、研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?21. 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题: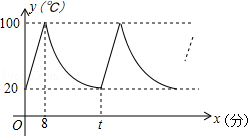 (1)、当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;(2)、求图中t的值;(3)、若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?22. 小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)、当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;(2)、求图中t的值;(3)、若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?22. 小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.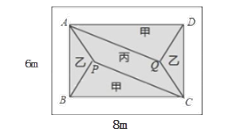 (1)、若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;(2)、若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
(1)、若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;(2)、若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.