广东省天河区普通高中2019届文数毕业班综合测试卷(二)
试卷更新日期:2019-04-28 类型:高考模拟
一、单选题
-
1. 若复数 是纯虚数,其中m是实数,则 = ( )A、i B、 C、 D、2. 已知全集 , , ,则图中阴影部分表示的集合是( )
 A、 B、 C、 D、3. 设等差数列 的前n项和为 ,若 , ,则 ( )A、63 B、45 C、39 D、274. 为保证树苗的质量,林业管理部门在每年3月12日植树节前都对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度 单位长度: ,其茎叶图如图所示,则下列描述正确的是( )
A、 B、 C、 D、3. 设等差数列 的前n项和为 ,若 , ,则 ( )A、63 B、45 C、39 D、274. 为保证树苗的质量,林业管理部门在每年3月12日植树节前都对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度 单位长度: ,其茎叶图如图所示,则下列描述正确的是( )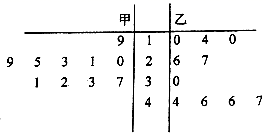 A、甲种树苗的平均高度大于乙种树苗的平均高度,甲种树苗比乙种树苗长得整齐 B、甲种树苗的平均高度大于乙种树苗的平均高度,乙种树苗比甲种树苗长得整齐 C、乙种树苗的平均高度大于甲种树苗的平均高度,乙种树苗比甲种树苗长得整齐 D、乙种树苗的平均高度大于甲种树苗的平均高度,甲种树苗比乙种树苗长得整齐5. 已知抛物线C: 的焦点为F,准线l与x轴的交点为A,M是抛物线C上的点,且 轴,若以AF为直径的圆截直线AM所得的弦长为2,则 ( )A、2 B、 C、4 D、6. 在 中, , ,则A、3 B、 C、 D、7. 已知命题p:若 , , ,则 :命题q:“ ”是“ ”的必要不充分条件,则下列命题为真命题的是( )A、 B、 C、 D、8. 若函数 (其中 , )图象的一个对称中心为 ,其相邻一条对称轴方程为 ,该对称轴处所对应的函数值为 ,为了得到 的图象,则只要将 的图象( )A、向右平移 个单位长度 B、向左平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度9. 已知数列 是 为首项, 为公差的等差数列, 是 为首项, 为公比的等比数列,设 , , ,则当 时, 的最大值是( )A、9 B、10 C、11 D、1210. 在同意直角坐标系中,函数 的图像不可能的是( )A、
A、甲种树苗的平均高度大于乙种树苗的平均高度,甲种树苗比乙种树苗长得整齐 B、甲种树苗的平均高度大于乙种树苗的平均高度,乙种树苗比甲种树苗长得整齐 C、乙种树苗的平均高度大于甲种树苗的平均高度,乙种树苗比甲种树苗长得整齐 D、乙种树苗的平均高度大于甲种树苗的平均高度,甲种树苗比乙种树苗长得整齐5. 已知抛物线C: 的焦点为F,准线l与x轴的交点为A,M是抛物线C上的点,且 轴,若以AF为直径的圆截直线AM所得的弦长为2,则 ( )A、2 B、 C、4 D、6. 在 中, , ,则A、3 B、 C、 D、7. 已知命题p:若 , , ,则 :命题q:“ ”是“ ”的必要不充分条件,则下列命题为真命题的是( )A、 B、 C、 D、8. 若函数 (其中 , )图象的一个对称中心为 ,其相邻一条对称轴方程为 ,该对称轴处所对应的函数值为 ,为了得到 的图象,则只要将 的图象( )A、向右平移 个单位长度 B、向左平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度9. 已知数列 是 为首项, 为公差的等差数列, 是 为首项, 为公比的等比数列,设 , , ,则当 时, 的最大值是( )A、9 B、10 C、11 D、1210. 在同意直角坐标系中,函数 的图像不可能的是( )A、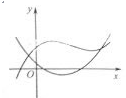 B、
B、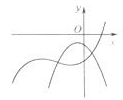 C、
C、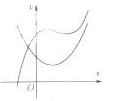 D、
D、 11. 已知双曲线C: 的左、右焦点分别为 , ,离心率为e,过点 的直线l与双曲线C的左、右两支分别交于A,B两点,若 ,且 ,则 ( )A、 B、 C、 D、12. 定义在 上的函数 满足 , ,则不等式 的解集为( )A、 B、 C、 D、
11. 已知双曲线C: 的左、右焦点分别为 , ,离心率为e,过点 的直线l与双曲线C的左、右两支分别交于A,B两点,若 ,且 ,则 ( )A、 B、 C、 D、12. 定义在 上的函数 满足 , ,则不等式 的解集为( )A、 B、 C、 D、二、填空题
-
13. 已知实数x,y满足不等式组 ,则 的最小值为 .14. 设定义在R上的函数满足 ,当 时, ,则 .15. 已知 为数列 的前n项和, , ,则 .16. 已知三棱锥 的体积为2, 是等腰直角三角形,其斜边 ,且三棱锥 的外接球的球心O恰好是AD的中点,则球O的体积为 .
三、解答题
-
17. 在 中,角A,B,C的对边分别为a,b,c,已知 .(1)、求角B的大小;(2)、若 ,点D在AC边上,且 , ,求c边的长.18. 汉字听写大会 不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试 现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组 ,第2组 , ,第6组 ,如图是按上述分组方法得到的频率分布直方图.
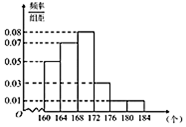 (1)、若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;(2)、试估计该市市民正确书写汉字的个数的平均数与中位数;(3)、已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.19. 如图,D是AC的中点,四边形BDEF是菱形,平面 平面ABC, , , .
(1)、若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;(2)、试估计该市市民正确书写汉字的个数的平均数与中位数;(3)、已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.19. 如图,D是AC的中点,四边形BDEF是菱形,平面 平面ABC, , , .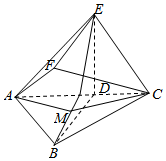 (1)、若点M是线段BF的中点,证明: 平面AMC;(2)、求六面体ABCEF的体积.20. 已知椭圆C: 的左右焦点分别为 , ,左顶点为A,上顶点为B,离心率为 , 的面积为 .(1)、求椭圆C的标准方程;(2)、过 的直线l与椭圆C相交于不同的两点M,N,求 内切圆半径的最大值.
(1)、若点M是线段BF的中点,证明: 平面AMC;(2)、求六面体ABCEF的体积.20. 已知椭圆C: 的左右焦点分别为 , ,左顶点为A,上顶点为B,离心率为 , 的面积为 .(1)、求椭圆C的标准方程;(2)、过 的直线l与椭圆C相交于不同的两点M,N,求 内切圆半径的最大值.