福建省厦门市2019届高中毕业班理数第一次（3月)质量检测试卷

试卷更新日期：2019-04-28 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知复数 $z$ 满足 $(z + 1) i = 3 + 2 i$ ，则 $| z | =$ （）

A、 $\sqrt{5}$ B、 $\sqrt{10}$ C、5 D、10

查看试题解析
2. 若抛物线 $x^{2} = a y$ 的焦点到准线的距离为1，则 $a =$ （）

A、2 B、4 C、 $\pm 2$ D、 $\pm 4$

查看试题解析
3. 已知集合 $A = {x | x^{2} - 4 x + 3 〉 0}$ ， $B = {x | x - a < 0}$ ，若 $B \subseteq A$ ，则实数 $a$ 的取值范围为（）

A、 $(3, + \infty)$ B、 $[3, + \infty)$ C、 $(- \infty, 1)$ D、 $(- \infty, 1]$

查看试题解析
4. 若 $x ， y$ 满足约束条件 ${\begin{matrix} x + y \geq 2 \\ 2 x - 3 y \leq 9 \\ x \geq 0 \end{matrix}$ ，则 $z = x + 2 y$ 的最小值为（）

A、-6 B、0 C、1 D、2

查看试题解析
5. 在梯形 $A B C D$ 中， $A B / / C D$ ， $A B = 4$ ， $B C = C D = D A = 2$ ，若 $E$ 为 $B C$ 的中点，则 $\overset{⇀}{A C} \cdot \overset{⇀}{A E} =$ （）

A、 $\sqrt{3}$ B、3 C、 $2 \sqrt{3}$ D、12

查看试题解析
6. 如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，其中俯视图为扇形，则该几何体的体积为（）

A、 $\frac{2 π}{3}$ B、 $\frac{4 π}{3}$ C、 $\frac{14 π}{3}$ D、 $\frac{16 π}{9}$

查看试题解析
7. 已知 $a > b > 0$ ， $x = a + b e^{b}$ ， $y = b + a e^{a}$ ， $z = b + a e^{b}$ ，则（）

A、 $x < z < y$ B、 $z < x < y$ C、 $z < y < x$ D、 $y < z < x$

查看试题解析
8. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $a_{1} = 1$ ， $2 S_{n} = a_{n + 1} a_{n}$ ，则 $S_{20} =$ （）

A、410 B、400 C、210 D、200

查看试题解析
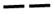9. 《易经》是中国传统文化中的精髓，下图是易经八卦图（含乾、坤、巽、震、坎、离、艮、兑八卦），每一卦由三根线组成（表示一根阳线，表示一根阴线），从八卦中任取两卦，这两卦的六根线中恰有三根阳线和三根阴线的概率为（）

A、 $\frac{1}{14}$ B、 $\frac{1}{7}$ C、 $\frac{5}{28}$ D、 $\frac{5}{14}$

查看试题解析
10. 已知函数 $f (x) = {\begin{matrix} x^{2} - 3 x + 2 ， x \leq 1 \\ l n x ， x > 1 \end{matrix}$ ， $g (x) = f (x) - a x + a$ ，若 $g (x)$ 恰有1个零点，则 $a$ 的取值范围是（）

A、 $[- 1 ， 0] \cup^{} [1 ， + \infty)$ B、 $(- \infty ， - 1] \cup^{} [0 ， 1]$ C、 $[- 1 ， 1]$ D、 $(- \infty ， - 1] \cup^{} [1 ， + \infty)$

查看试题解析
11. 已知函数 $f (x) = sin (2 x - \frac{π}{3})$ ，若方程 $f (x) = \frac{1}{3}$ 在 $(0 ， π)$ 的解为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，则 $sin (x_{1} - x_{2}) =$ （）

A、 $- \frac{2 \sqrt{2}}{3}$ B、 $- \frac{\sqrt{3}}{2}$ C、 $- \frac{1}{2}$ D、 $- \frac{1}{3}$

查看试题解析
12. 已知双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的一个焦点为 $F$ ，点 $A, B$ 是 $C$ 的一条渐近线上关于原点对称的两点，以 $A B$ 为直径的圆过 $F$ 且交 $C$ 的左支于 $M, N$ 两点，若 $|MN|=2$ ， $Δ A B F$ 的面积为8，则 $C$ 的渐近线方程为（）

A、 $y = \pm \sqrt{3} x$ B、 $y = \pm \frac{\sqrt{3}}{3} x$ C、 $y = \pm 2 x$ D、 $y = \pm \frac{1}{2} x$

查看试题解析

二、填空题

13. 在等比数列 ${a_{n}}$ 中， $a_{2} = 1$ ， $a_{3} a_{5} = 2 a_{7}$ ，则 $a_{n} =$ ．

查看试题解析
14. $(1 + \frac{1}{x}) {(1 - 2 x)}^{5}$ 的展开式中 $x^{2}$ 的系数为．

查看试题解析
15. 已知函数 $f (x) = e^{x} - e^{- x} - 1$ ，则关于 $x$ 的不等式 $f (2 x) + f (x + 1) > - 2$ 的解集为．

查看试题解析
16. 已知正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的所有棱长为2，点 $M, N$ 分别在侧面 $A B B_{1} A_{1}$ 和 $A C C_{1} A_{1}$ 内， $B C_{1}$ 与 $B_{1} C$ 交于点 $P$ ，则 $Δ M N P$ 周长的最小值为．

查看试题解析

三、解答题

17. 在平面四边形 $A B C D$ 中， $∠ A B C = \frac{π}{3}$ ， $∠ A D C = \frac{π}{2}$ ， $B C = 2$ .

(1)、若 $Δ A B C$ 的面积为 $\frac{3 \sqrt{3}}{2}$ ，求 $A C$ ；

(2)、若 $A D = 2 \sqrt{3}$ ， $∠ A C B = ∠ A C D + \frac{π}{3}$ ，求 $tan ∠ A C D$ .

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中， $B C ⊥ C D$ ， $A D = C D$ ， $P A = 3 \sqrt{2}$ ， $Δ A B C$ 和 $Δ P B C$ 均为边长为 $2 \sqrt{3}$ 的等边三角形.

(1)、求证：平面 $P B C ⊥$ 平面 $A B C D$ ；

(2)、求二面角 $C - P B - D$ 的余弦值.

查看试题解析

19. 某公司生产一种产品，从流水线上随机抽取100件产品，统计其质量指数并绘制频率分布直方图（如图1）：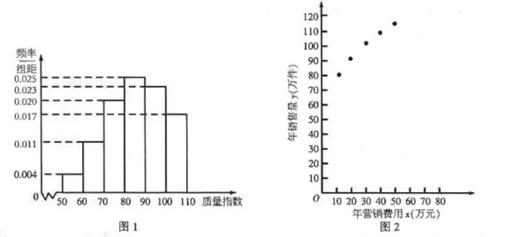

产品的质量指数在 $[50 ， 70)$ 的为三等品，在 $[70 ， 90)$ 的为二等品，在 $[90 ， 110]$ 的为一等品，该产品的三、二、一等品的销售利润分别为每件1.5，3.5，5.5（单位：元），以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.

(1)、求每件产品的平均销售利润；

(2)、该公司为了解年营销费用

x

（单位：万元）对年销售量

y

（单位：万件）的影响，对近5年的年营销费用

x_{i}

和年销售量

y_{i}

(i = 1 ， 2 ， 3 ， 4 ， 5)

数据做了初步处理，得到的散点图（如图2）及一些统计量的值.

$\sum_{i = 1}^{5} u_{i}$	$\sum_{i = 1}^{5} v_{i}$	$\sum_{i = 1}^{5} (u_{i} - \bar{u}) (v_{i} - \bar{v})$	$\sum_{i = 1}^{5} {(u_{i} - \bar{u})}^{2}$
16.30	24.87	0.41	1.64

表中 $u_{i} = ln x_{i}$ ， $v_{i} = ln y_{i}$ ， $\bar{u} = \frac{1}{5} \sum_{i = 1}^{5} u_{i}$ ， $\bar{v} = \frac{1}{5} \sum_{i = 1}^{5} v_{i}$

根据散点图判断， $y = a \cdot x^{b}$ 可以作为年销售量 $y$ （万件）关于年营销费用 $x$ （万元）的回归方程.

（ⅰ）建立 $y$ 关于 $x$ 的回归方程；

（ⅱ）用所求的回归方程估计该公司应投入多少营销费，才能使得该产品一年的收益达到最大？（收益=销售利润-营销费用，取 $e^{4.159} = 64$ ）

参考公式：对于一组数据： $(u_{1} ， v_{1})$ ， $(u_{2} ， v_{2})$ ， $\dots$ ， $(u_{n} ， v_{n})$ ，其回归直线 $v = α + β u$ 的斜率和截距的最小乘估计分别为 $\hat{β} = \frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}}$ ， $\overset{\land}{α} = \overset{\land}{v} - \hat{β} \bar{u}$

查看试题解析

20. 已知 $O$ 为坐标原点， $F$ 为椭圆 $C ： \frac{x^{2}}{4} + \frac{y^{2}}{9} = 1$ 的上焦点， $C$ 上一点 $A$ 在 $x$ 轴上方，且 $| O A | = \sqrt{5}$ .

(1)、求直线 $A F$ 的方程；

(2)、 $B$ 为直线 $A F$ 与 $C$ 异于 $A$ 的交点， $C$ 的弦 $M N$ ， $A B$ 的中点分别为 $P ， Q$ ，若 $O ， P ， Q$ 在同一直线上，求 $Δ O M N$ 面积的最大值.

查看试题解析
21. 已知函数 $f (x) = (x + a) ln (x + 1) - a x$ .

(1)、若 $a = 2$ ，求 $f (x)$ 的单调区间；

(2)、若 $a \leq - 2$ ， $- 1 < x < 0$ ，求证： $f (x) > 2 x (1 - e^{- x})$ .

查看试题解析
22. 在直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{matrix} x = t c o s α \\ y = t s i n α \end{matrix}$ （ $t$ 为参数），以坐标原点 $O$ 为极点，以 $x$ 轴正半轴为极轴，建立极坐标系，曲线 $C$ 的极坐标方程为 $ρ^{2} = \frac{4}{1 + 3 {sin}^{2} θ}$ .

(1)、求 $l$ 的普通方程和 $C$ 的直角坐标方程；

(2)、若 $C$ 上恰有2个点到 $l$ 的距离等于 $\sqrt{2}$ ，求 $l$ 的斜率.

查看试题解析
23. 已知函数 $f (x) = | x + 2 | + | x - 4 |$ .

(1)、求不等式 $f (x) \leq 3 x$ 的解集；

(2)、若 $f (x) \geq k (x - 1)$ 对任意 $x \in R$ 恒成立，求 $k$ 的取值范围.

查看试题解析