2018-2019学年初中数学浙教版七年级下册5.5分式方程 同步练习
试卷更新日期:2019-04-28 类型:同步测试
一、单选题
-
1. 九年级学生去距学校10km的博物馆参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为xkm/h,则所列方程正确的是( )A、
 =
=  ﹣
B、
﹣
B、 =
=  ﹣20
C、
﹣20
C、 =
=  +
D、
+
D、 =
=  +20
2. 用换元法解分式方程 ﹣ =5时,设 =y,原方程变形为( )A、2y2﹣5y﹣3=0 B、6y2+10y﹣1=0 C、3y2+5y﹣2=0 D、y2﹣10y﹣6=03. 解分式方程 =3时,去分母后变形为( )A、2-(x+2)=3 B、2+(x+2)=3 C、2+(x+2)=3(x-1) D、2-(x+2)=3(x-1)4. “五·一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每名同学比原来少摊了3元钱车费,设原来参加游览的同学共x名,则所列方程为( )A、
+20
2. 用换元法解分式方程 ﹣ =5时,设 =y,原方程变形为( )A、2y2﹣5y﹣3=0 B、6y2+10y﹣1=0 C、3y2+5y﹣2=0 D、y2﹣10y﹣6=03. 解分式方程 =3时,去分母后变形为( )A、2-(x+2)=3 B、2+(x+2)=3 C、2+(x+2)=3(x-1) D、2-(x+2)=3(x-1)4. “五·一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每名同学比原来少摊了3元钱车费,设原来参加游览的同学共x名,则所列方程为( )A、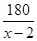 -
-  =3
B、
=3
B、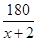 -
-  =3
C、
=3
C、 -
- 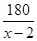 =3
D、
=3
D、 -
- 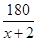 =3
5. 某开发区在一项工程招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程,刚好如 期完成;②乙队单独完成此项工程要比规定工期多用5天;③
=3
5. 某开发区在一项工程招标时,接到甲、乙两个工程队的投标书,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程,刚好如 期完成;②乙队单独完成此项工程要比规定工期多用5天;③ ,剩下的工程由乙队单独做,也正好如期完工.小亮设规定的工期为x天,根据题意列出了方 程: ,则方案③中被墨水污染的部分应该是( ) A、甲先做了4天 B、甲乙合作了4天 C、甲先做了工程的 D、甲乙合作了工程的6. 已知关于 的分式方程 的解是正数,则 的取值范围是( )A、
,剩下的工程由乙队单独做,也正好如期完工.小亮设规定的工期为x天,根据题意列出了方 程: ,则方案③中被墨水污染的部分应该是( ) A、甲先做了4天 B、甲乙合作了4天 C、甲先做了工程的 D、甲乙合作了工程的6. 已知关于 的分式方程 的解是正数,则 的取值范围是( )A、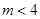 且
且 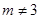 B、
B、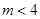 C、
C、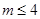 且
且 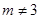 D、
D、 且
且  7. 把分式方程 化为整式方程,正确的是( )A、x + 2 = -1 B、x + 2(x - 2)=1 C、x +2(x-2)=﹣1 D、x + 2 = - 18. 关于x的方程 =2+ 无解,则k的值为( )A、±3 B、3 C、 D、无法确定9. 关于x的分式方程 的解是负数,则m的取值范围是( )A、
7. 把分式方程 化为整式方程,正确的是( )A、x + 2 = -1 B、x + 2(x - 2)=1 C、x +2(x-2)=﹣1 D、x + 2 = - 18. 关于x的方程 =2+ 无解,则k的值为( )A、±3 B、3 C、 D、无法确定9. 关于x的分式方程 的解是负数,则m的取值范围是( )A、 B、
B、 且
且 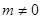 C、
C、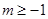 D、
D、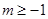 且
且 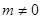 10. 下列各式中:
10. 下列各式中:①由3x=-4系数化为1得x=- ;②由5=2-x移项得x=5-2;③由 去分母得2(2x-1)=1+3(x-3);④由2(2x-1)-3(x-3)=1去括号得4x-2-3x-9=1.其中正确的个数有( )
A、0个 B、1个 C、3个 D、4个二、填空题
-
11. 已知关于x的分式方程 有增根,则a=.12. 若分式 有增根,则 m=;13. 若方程 无解,则m .14. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,现在平均每天生产台机器.15. 设A、B、C为三个连续的正偶数,若A的倒数与C的倒数的2倍之和等于B的倒数的3倍.设B数为 ,则所列方程是 .16. 若关于x的方程 + = 无解,则m的值为 .
三、解答题
-
17. 解方程:(1)、 =1(2)、 .18. 已知 的解为正数,求m的取值范围.
关于这道题,有位同学作出如下解答:
解:去分母得,x-2(x-3)=m,
化简,得-x=m-6,
故x=-m+6.
要使方程的根为正数,必须-m+6>0,
得m<6.
所以,当m<6时,方程 的解是正数.
(1)、写出第一步变形的依据 .(2)、上述解法是否有误?若有错误请说明错误的原因,并写出正确解答;若没有错误请说明其余每一步解法的依据.19. 某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用6000元购进电冰箱的数量与用4800元购进空调的数量相等.(1)、求每台电冰箱与空调的进价分别是多少?(2)、已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,现有两种进货方案①冰箱30台,空调70台;②冰箱50台,空调50台,那么该商店要获得最大利润应如何进货?20. 某农场为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?21. 阅读下列材料:关于x的分式方程x+ =c+ 的解是x1=c,x2=
x- = c- ,即x+ =c+ 的解是x1=c,x2= ;
x+ =c+ 的解是x1=c,x2= ;
x+ =c+ 的解是x1=c,x2= .
请观察上述方程与解的特征,比较关于x的方程x+ =c+ (m≠0)与它的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
由上述的观察、比较、猜想、验证,可以得出结论;
如果方程的左边是未知数与其倒数的倍数的和,方程右边形式与左边的完全相同,只是把其中未知数换成某个常数,那么这样的方程可以直接得解.
请利用这个结论解关于x的方程: