2013年广西玉林市中考数学试卷

试卷更新日期：2017-05-15 类型：中考真卷

进入出卷网下载

一、选择题

1. 2的相反数是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 若∠α=30°，则∠α的补角是（　　）

A、30° B、60° C、120° D、150°

查看试题解析
3. 我国第一艘航母“辽宁舰”最大排水量为67500吨，用科学记数法表示这个数字是（　　）

A、6.75×10³吨 B、67.5×10³吨 C、6.75×10⁴吨 D、6.75×10⁵吨

查看试题解析
4. 直线c与a、b均相交，当a∥b时（如图），则（　　）

A、∠1＞∠2 B、∠1＜∠2 C、∠1=∠2 D、∠1+∠2=90°

查看试题解析
5. 在数轴上表示不等式x+5≥1的解集，正确的是（　　）

A、 B、 C、 D、

查看试题解析
6. 已知一组从小到大的数据：0，4，x，10的中位数是5，则x=（　　）

A、5 B、6 C、7 D、8

查看试题解析
7. 某几何体的三视图如图所示，则组成该几何体共用了（　　）小方块．

A、12块 B、9块 C、7块 D、6块

查看试题解析
8. 如图是某手机店今年1﹣5月份音乐手机销售额统计图．根据图中信息，可以判断相邻两个月音乐手机销售额变化最大的是（　　）

A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月

查看试题解析
9. 方程 $\frac{1}{x - 1} - \frac{3}{x + 1} = 0$ 的解是（　　）

A、x=2 B、x=1 C、x= $\frac{1}{2}$ D、x=﹣2

查看试题解析
10. 如图，在给定的一张平行四边形纸片上作一个菱形．甲、乙两人的作法如下：
甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．
乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形．
根据两人的作法可判断（　　）

A、甲正确，乙错误 B、乙正确，甲错误 C、甲、乙均正确 D、甲、乙均错误

查看试题解析
11. 一列数a₁ ， a₂ ， a₃ ， …，其中a₁= $\frac{1}{2}$ ，a_n= $\frac{1}{1 - a_{n - 1}}$ （n为不小于2的整数），则a₁₀₀=（　　）

A、 $\frac{1}{2}$ B、2 C、﹣1 D、﹣2

查看试题解析
12. 均匀地向一个瓶子注水，最后把瓶子注满．在注水过程中，水面高度h随时间t的变化规律如图所示，则这个瓶子的形状是下列的（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

13. |﹣1|= ．

查看试题解析
14. 化简： $\frac{3}{\sqrt{5}}$ = ．

查看试题解析
15. 分解因式：x²﹣9= ．

查看试题解析
16. 如图，实线部分是半径为15m的两条等弧组成的游泳池，若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长是m．

查看试题解析
17. 如图，在直角坐标系中，O是原点，已知A（4，3），P是坐标轴上的一点，若以O，A，P三点组成的三角形为等腰三角形，则满足条件的点P共有个，写出其中一个点P的坐标是．

查看试题解析
18. 如图，△ABC是⊙O内接正三角形，将△ABC绕点O顺时针旋转30°得到△DEF，DE分别交AB，AC于点M，N，DF交AC于点Q，则有以下结论：①∠DQN=30°；②△DNQ≌△ANM；③△DNQ的周长等于AC的长；④NQ=QC．其中正确的结论是．（把所有正确的结论的序号都填上）

查看试题解析

三、解答题

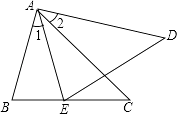
19. 计算： $\sqrt[3]{8}$ 2cos60°﹣（π﹣2^﹣¹）⁰ ．

查看试题解析
20. 如图，AB=AE，∠1=∠2，∠C=∠D．
求证：△ABC≌△AED．

查看试题解析
21. 已知关于x的方程x²+x+n=0有两个实数根﹣2，m．求m，n的值．

查看试题解析
22. 某小区为了促进生活垃圾的分类处理，将生活垃圾分为：可回垃圾、厨余垃圾、其他垃圾三类，分别记为A，B，C：并且设置了相应的垃圾箱，依次记为a，b，c．

(1)、若将三类垃圾随机投入三个垃圾箱，请你用树形图的方法求垃圾投放正确的概率：

(2)、为了调查小区垃圾分类投放情况，现随机抽取了该小区三类垃圾箱中总重500kg生活垃圾，数据如下（单位：）
a
b
c
A
40
15
10
B
60
250
40
C
15
15
55
试估计“厨余垃圾”投放正确的概率．

查看试题解析
23. 如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，若AC=FC．

(1)、求证：AC是⊙O的切线：

(2)、若BF=8，DF= $\sqrt{40}$ ，求⊙O的半径r．

查看试题解析
24. 工匠制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料烧到800℃，然后停止煅烧进行锻造操作，经过8min时，材料温度降为600℃．煅烧时温度y（℃）与时间x（min）成一次函数关系；锻造时，温度y（℃）与时间x（min）成反比例函数关系（如图）．已知该材料初始温度是32℃．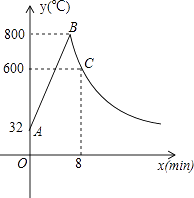

(1)、分别求出材料煅烧和锻造时y与x的函数关系式，并且写出自变量x的取值范围；

(2)、根据工艺要求，当材料温度低于480℃时，须停止操作．那么锻造的操作时间有多长？

查看试题解析
25. 如图，在直角梯形ABCD中，AD∥BC，AD⊥DC，点A关于对角线BD的对称点F刚好落在腰DC上，连接AF交BD于点E，AF的延长线与BC的延长线交于点G，M，N分别是BG，DF的中点．

(1)、求证：四边形EMCN是矩形；

(2)、若AD=2，S_梯形_ABCD= $\frac{15}{2}$ ，求矩形EMCN的长和宽．

查看试题解析
26.
如图，抛物线y=﹣（x﹣1）²+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．

(1)、求点B，C的坐标；

(2)、判断△CDB的形状并说明理由；

(3)、将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．

查看试题解析

	a	b	c
A	40	15	10
B	60	250	40
C	15	15	55