2013年广西南宁市中考数学试卷

试卷更新日期：2017-05-15 类型：中考真卷

进入出卷网下载

一、选择题

1. 在﹣2，1，5，0这四个数中，最大的数是（）

A、﹣2 B、1 C、5 D、0

查看试题解析
2. 如图所示，将平面图形绕轴旋转一周，得到的几何体是（　　）

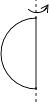A、 B、 C、 D、

查看试题解析
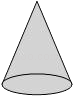3. 2013年6月11日，神舟十号飞船发射成功，神舟十号飞船身高9米，重约8吨，飞行速度约每秒7900米，将数7900用科学记数法表示，表示正确的是（　　）

A、0.79×10⁴ B、7.9×10⁴ C、7.9×10³ D、0.79×10³

查看试题解析
4. 小乐用一块长方形硬纸板在阳光下做投影实验，通过观察，发现这块长方形硬纸板在平整的地面上不可能出现的投影是（　　）

A、三角形 B、线段 C、矩形 D、平行四边形

查看试题解析
5. 甲、乙、丙、丁四名选手参加100米决赛，赛场只设1、2、3、4四个跑道，选手以随机抽签的方式决定各自的跑道，若甲首先抽签，则甲抽到1号跑道的概率是（　　）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
6. 若分式 $\frac{x - 2}{x + 1}$ 的值为0，则x的值为（　　）

A、﹣1 B、0 C、2 D、﹣1或2

查看试题解析
7. 如图，圆锥形的烟囱底面半径为15cm，母线长为20cm，制作这样一个烟囱帽所需要的铁皮面积至少是（　　）

A、1500πcm² B、300πcm² C、600πcm² D、150πcm²

查看试题解析
8. 下列各式计算正确的是（　　）

A、3a³+2a²=5a⁶ B、 $2 \sqrt{a} + \sqrt{a} = 3 \sqrt{a}$ C、a⁴•a²=a⁸ D、（ab²）³=ab⁶

查看试题解析
9. 陈老师打算购买气球装扮学校“六一”儿童节活动会场，气球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同，由于会场布置需要，购买时以一束（4个气球）为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为（　　）

A、19 B、18 C、16 D、15

查看试题解析
10. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列说法错误的是（　　）

A、图象关于直线x=1对称 B、函数y=ax²+bx+c（a≠0）的最小值是﹣4 C、﹣1和3是方程ax²+bx+c=0（a≠0）的两个根 D、当x＜1时，y随x的增大而增大

查看试题解析
11. 如图，AB是⊙O的直径，弦CD交AB于点E，且AE=CD=8，∠BAC= $\frac{1}{2}$ ∠BOD，则⊙O的半径为（　　）

A、4 $\sqrt{2}$ B、5 C、4 D、3

查看试题解析
12.
如图，直线y= $\frac{1}{2} x$ 与双曲线y= $\frac{k}{x}$ （k＞0，x＞0）交于点A，将直线y= $\frac{1}{2} x$ 向上平移4个单位长度后，与y轴交于点C，与双曲线y= $\frac{k}{x}$ （k＞0，x＞0）交于点B，若OA=3BC，则k的值为（　　）

A、3 B、6 C、 $\frac{9}{4}$ D、 $\frac{9}{2}$

查看试题解析

二、填空题.

13. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
14. 一副三角板如图所示放置，则∠AOB=°．

查看试题解析
15. 分解因式：x²﹣25= ．

查看试题解析
16. 某中学规定：学生的学期体育综合成绩满分为100分，其中，期中考试成绩占40%，期末考试成绩占60%，小海这个学期的期中、期末成绩（百分制）分别是80分、90分，则小海这个学期的体育综合成绩是分．

查看试题解析
17. 有这样一组数据a₁ ， a₂ ， a₃ ， …a_n ，满足以下规律： $a_{1} = \frac{1}{2} ， a_{2} = \frac{1}{1 - a_{1}} ， a_{3} = \frac{1}{1 - a_{2}} ， ... ， a_{n} = \frac{1}{1 - a_{n - 1}}$ （n≥2且n为正整数），则a₂₀₁₃的值为（结果用数字表示）．

查看试题解析
18. 如图，在边长为2的正三角形中，将其内切圆和三个角切圆（与角两边及三角形内切圆都相切的圆）的内部挖去，则此三角形剩下部分（阴影部分）的面积为．

查看试题解析

三、解答题。

19. 计算：2013⁰﹣ $\sqrt{27}$ +2cos60°+（﹣2）

查看试题解析
20. 先化简，再求值： $(\frac{x}{x - 1} + \frac{1}{x - 1}) \div \frac{x + 1}{x^{2} - 2 x + 1}$ ，其中x=﹣2．

查看试题解析
21.
如图，△ABC三个定点坐标分别为A（﹣1，3），B（﹣1，1），C（﹣3，2）．

(1)、请画出△ABC关于y轴对称的△A₁B₁C₁；

(2)、以原点O为位似中心，将△A₁B₁C₁放大为原来的2倍，得到△A₂B₂C₂ ，请在第三象限内画出△A₂B₂C₂ ，并求出 $S_{△ A_{1} B_{1} C_{1}} ： S_{△ A_{2} B_{2} C_{2}}$ 的值．

查看试题解析
22. 2013年6月，某中学结合广西中小学阅读素养评估活动，以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：

(1)、在这次抽样调查中，一共调查了多少名学生？

(2)、请把折线统计图（图1）补充完整；

(3)、求出扇形统计图（图2）中，体育部分所对应的圆心角的度数；

(4)、如果这所中学共有学生1800名，那么请你估计最喜爱科普类书籍的学生人数．

查看试题解析
23. 如图，在菱形ABCD中，AC为对角线，点E、F分别是边BC、AD的中点．

(1)、求证：△ABE≌△CDF；

(2)、若∠B=60°，AB=4，求线段AE的长．

查看试题解析
24. 在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时x（h）之间的函数图象，根据图象解答以下问题：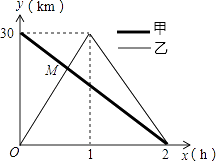

(1)、写出A、B两地之间的距离；

(2)、求出点M的坐标，并解释该点坐标所表示的实际意义；

(3)、若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．

查看试题解析
25. 如图，在△ABC中，∠BAC=90°，AB=AC，AB是⊙O的直径，⊙O交BC于点D，DE⊥AC于点E，BE交⊙O于点F，连接AF，AF的延长线交DE于点P．

(1)、求证：DE是⊙O的切线；

(2)、求tan∠ABE的值；

(3)、若OA=2，求线段AP的长．

查看试题解析
26.
如图，抛物线y=ax²+c（a≠0）经过C（2，0），D（0，﹣1）两点，并与直线y=kx交于A、B两点，直线l过点E（0，﹣2）且平行于x轴，过A、B两点分别作直线l的垂线，垂足分别为点M、N．

(1)、求此抛物线的解析式；

(2)、求证：AO=AM；

(3)、探究：
①当k=0时，直线y=kx与x轴重合，求出此时 $\frac{1}{A M}$ + $\frac{1}{B N}$ 的值；
②试说明无论k取何值， $\frac{1}{A M}$ + $\frac{1}{B N}$ 的值都等于同一个常数．

查看试题解析