浙江省湖州市2019年中考数学预测卷
试卷更新日期:2019-04-26 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 下列四个数中,与-5的和为0的数是( )A、-5 B、5 C、0 D、-2. 计算2x3•x2的结果是( )A、2x5 B、2x6 C、3x5 D、3x63. 一个由相同小正方体堆积而成的几何体如图所示,从正面看,该几何体的形状图是( ).
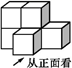 A、
A、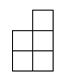 B、
B、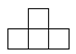 C、
C、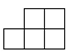 D、
D、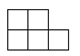 4. 某次数学趣味竞赛共有10道题目,每道题答对得10分,答错或不答得0分.
4. 某次数学趣味竞赛共有10道题目,每道题答对得10分,答错或不答得0分.人数
2
5
13
10
7
3
成绩(分)
50
60
70
80
90
100
全班40名同学的成绩的中位数和众数分别是( )
A、75,70 B、70,70 C、80,80 D、75,805. 在△ABC中,AB=AC,∠A=40°,点D在AB上,若CD=AD,则∠BCD的大小是( )A、25° B、30° C、40° D、45°6. 已知直线 与双曲线 的一个交点的坐标为 ,则它们的另一个交点的坐标是( )A、(-1, -3) B、(-1, 3) C、(1, -3) D、(1, 3)7. 把同一副扑克牌中的红桃 、红桃 、红桃 三张牌背面朝上放在桌子上,从中随机抽取两张,牌面的数字之和为奇数的概率为( )A、 B、 C、 D、8. 如图,在△ABC中,AB=AC,∠BAC=70°,∠BAC的平分线与AB的垂直平分线交于点O,点E、F分别在BC、AC上,点C沿EF折叠后与点O重合,则∠BEO的度数是( ) A、20° B、35° C、40° D、55°9. 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6 ,则EH的长为( )
A、20° B、35° C、40° D、55°9. 如图,正六边形ABCDEF内接于⊙O,连结AC,EB,CH=6 ,则EH的长为( )
 A、12 B、18 C、6 +6 D、1210. 老师出示了小黑板上的题后(如图),小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被x轴截得的线段长为2.你认为四人的说法中,正确的有( )
A、12 B、18 C、6 +6 D、1210. 老师出示了小黑板上的题后(如图),小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被x轴截得的线段长为2.你认为四人的说法中,正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本题有6小题,每小题4分,共24分)
-
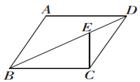
11. 二次根式 中字母x的取值范围是12. 若分式 的值为0,则a=.13. 如图,在菱形ABCD中,过点C作CE⊥BC交对角线BD于点E,且DE=CE,若 ,则DE=.
 14.
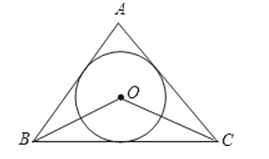
14.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=(填度数).
 15. 在一个不透明的盒子里装有5个分别写有数字﹣2,﹣1,1,2,3的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,将该数的绝对值作为点P的纵坐标,则点P落在抛物线y=﹣x2+2x+4与x轴所围成的区域内(不含边界)的概率是 .16. 如图,在正方形网格上有6个斜三角形:
15. 在一个不透明的盒子里装有5个分别写有数字﹣2,﹣1,1,2,3的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,将该数的绝对值作为点P的纵坐标,则点P落在抛物线y=﹣x2+2x+4与x轴所围成的区域内(不含边界)的概率是 .16. 如图,在正方形网格上有6个斜三角形: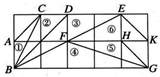
①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
在②~⑥中,与①相似的三角形的序号是.(把你认为正确的都填上)
三、解答题(本题有8小题,共66分)
-
17.
(1)、计算:( -3+ - )÷(- )(2)、化简:( - )÷18. 解不等式组 ,并把它的解集表示在数轴上.19. 已知二次函数的图象与x轴交于A(-2,0)、B(3,0)两点,且函数有最大值是2.(1)、求二次函数的图象的解析式;(2)、设此二次函数的顶点为P,求△ABP的面积.20. 图①表示的是某商场2012年前四个月中两个月的商品销售额的情况,图②表示的是商场家电部各月销售额占商场当月销售总额的百分比情况,观察图①、图②解答下列问题: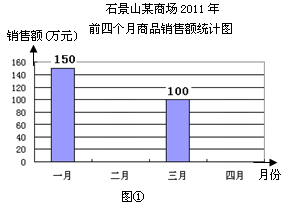
 (1)、商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;(2)、若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;(3)、小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由21. 如图, 是 的直径,过O作弦AC的垂线,交 于点D,分别交AE、AC于点E、点F,已知 .
(1)、商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;(2)、若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;(3)、小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由21. 如图, 是 的直径,过O作弦AC的垂线,交 于点D,分别交AE、AC于点E、点F,已知 . (1)、判断AE与 的位置关系,并说明理由;(2)、若 , ,求 的长.22. 一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数,若售价30元,能卖200台/月,若售价35元,能卖150台/月.(1)、求y与x的函数关系式.(2)、为清理库存,在不赔钱的情况下,售价定为多少元时,每月可获得最大销售量?(3)、如果想要每月获得2000元的利润,那么销售单价应定为多少元?23. 如图,在 中, , ,DF是 的中位线,点C关于DF的对称点为E,以DE,EF为邻边构造矩形DEFG,DG交BC于点H,连结CG.
(1)、判断AE与 的位置关系,并说明理由;(2)、若 , ,求 的长.22. 一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数,若售价30元,能卖200台/月,若售价35元,能卖150台/月.(1)、求y与x的函数关系式.(2)、为清理库存,在不赔钱的情况下,售价定为多少元时,每月可获得最大销售量?(3)、如果想要每月获得2000元的利润,那么销售单价应定为多少元?23. 如图,在 中, , ,DF是 的中位线,点C关于DF的对称点为E,以DE,EF为邻边构造矩形DEFG,DG交BC于点H,连结CG.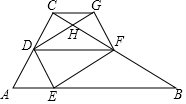 (1)、求证: ≌(2)、若 .
(1)、求证: ≌(2)、若 .求CG的长.
在 的边上取一点P,在矩形DEFG的边上取一点Q,若以P,Q,C,G为顶点的四边形是平行四边形,求出所有满足条件的平行四边形的面积.
(3)、在 内取一点O,使四边形AOHD是平行四边形,连结OA,OB,OC,直接写出 , , 的面积之比.24. Rt△ABC在直角坐标系内的位置如图所示,反比例函数 在第一象限内的图象与BC边交于点D(4,m),与AB边交于点E(2,n),△BDE的面积为2.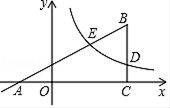 (1)、求m与n的数量关系;(2)、当 时,求反比例函数的解析式和直线AB的解析式;(3)、设P是线段AB边上的点,在(2)的条件下,是否存在点P,以B、C、P为顶点的三角形与△EDB相似?若存在,求出此时点P的坐标;若不存在,请说明理由.
(1)、求m与n的数量关系;(2)、当 时,求反比例函数的解析式和直线AB的解析式;(3)、设P是线段AB边上的点,在(2)的条件下,是否存在点P,以B、C、P为顶点的三角形与△EDB相似?若存在,求出此时点P的坐标;若不存在,请说明理由.