浙江省杭州市2019年中考数学预测卷3

试卷更新日期：2019-04-26 类型：中考模拟

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 绝对值大于1而小于3的整数是（）

A、±1 B、±2 C、±3 D、±4

查看试题解析
2. 十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从54万亿元增长80万亿元，稳居世界第二，其中80万亿用科学记数法表示为（）

A、8×10¹² B、8×10¹³ C、8×10¹⁴ D、0.8×10¹³

查看试题解析
3. $\sqrt{\frac{9}{4}}$ 的值等于（）

A、 $\frac{3}{2}$ B、﹣ $\frac{3}{2}$ C、± $\frac{3}{2}$ D、 $\frac{81}{16}$

查看试题解析
4. 下列说法正确的是（）

A、一组数据的中位数一定等于该组数据中的某个数据 B、一组数据的平均数和中位数一定不相等 C、一组数据的众数可以有几个 D、一组数据的方差一定大于这组数据的标准差

查看试题解析
5. 如图所示，直线AB与直线CD相交于点O，EO⊥AB，∠EOD＝25°，则下列说法正确的是（）

A、∠AOE与∠BOC互为对顶角 B、图中有两个角是∠EOD的邻补角 C、线段DO大于EO的理由是垂线段最短 D、∠AOC＝65°

查看试题解析
6. 如图为某商店的宣传单，小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子，共节省500元，则根据题意所列方程正确的是（）

A、0.6x+0.4y+100＝500 B、0.6x+0.4y﹣100＝500 C、0.4x+0.6y+100＝500 D、0.4x+0.6y﹣100＝500

查看试题解析
7. 在一个不透明的袋中装有10个只有颜色不同的球，其中5个红球、3个黄球和2个白球．从袋中任意摸出一个球，是白球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{3}{10}$ D、 $\frac{1}{5}$

查看试题解析
8. 如图，矩形ABCD的对角线相交于点O，AB＝10，∠ACB＝30°，则三角形AOD的面积是（）

A、25 $\sqrt{3}$ B、50 $\sqrt{3}$ C、100 D、100 $\sqrt{3}$

查看试题解析
9. 二次函数y＝ax²+bx+c（a、b、c为常数，且a≠0）中x与y的部分对应值如下表：
x
﹣2
﹣1
0
1
2
3
4
y
5
0
﹣3
﹣4
﹣3
0
5
给出以下三个结论：
（1）二次函数y＝ax²+bx+c最小值为﹣4；（2）若y＜0，则x的取值范围是0＜x＜2；（3）二次函数y＝ax²+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧，则其中正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
10. 如图，△ABC中，点D，E分别在AB，AC上，∠ADE＝∠C，如果AE＝4，△ADE的面积为5，四边形BCED的面积为15，那么AB的长为（）

A、6 B、 $\frac{20}{3}$ C、8 D、 $\frac{25}{3}$

查看试题解析

二、填空题（每小题4分，共24分）

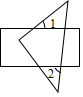
11. 如果单项式3x^a+2y^b^﹣2与5x³y^a+2的和为8x³y^a+2 ，那么a﹣b＝．

查看试题解析
12. 将一个含有45°角的直角三角板摆放在矩形上，如图所示，若∠1＝40°，则∠2＝．

查看试题解析
13. 若x+y＝3，xy＝﹣2，则x²y+y²x＝．

查看试题解析
14. 如图，AB为⊙O的直径，C为圆上（除A、B外）一动点，∠ACB的角平分线交⊙O于D，若AC＝8，BC＝6，则BD的长为．

查看试题解析
15. 星期天，小明上午8：00从家里出发，骑车到图书馆去借书，再骑车回到家．他离家的距离y（千米）与时间t（分钟）的关系如图所示，则上午8：45小明离家的距离是千米．

查看试题解析
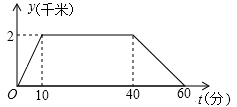16. 如图，将长方形纸片ABCD分别沿EF，EB翻折，点D恰好落在AB边上，点C恰好落在D'E上，若FD＝5，DE＝10，BC＝8，则EC的长度为．

查看试题解析

三、解答题（7小题，共66分）

17. 某市一蔬菜生产基础用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种，图中是某天恒温系统从开启到关闭及关闭后，大棚内温度y（℃）随时间x（h）变化的函数图象，其中AB段是恒温阶段，BC是双曲线y＝ $\frac{k}{x}$ 的一部分．请根据图中的信息解答下列问题：

(1)、求k的值；

(2)、恒温系统在一天内保持大鹏温度在15℃及15℃以上的时间有多少小时？

查看试题解析

18. 新学期开学时，某校对八年级学生掌握“中学生日常行为规范”的情况进行了知识测试测试成绩全部合格（说明：成绩大于或等于60分合格），学校随机选取了部分学生的成绩，整理并绘制成以下不完整的图表：

部分学生测试成绩统计表

分数段	频数	频率
60≤x＜70	9	a
70≤x＜80	36	0.4
80≤x＜90	27	b
90≤x≤100	C	0.2

请根据上述统计图表，解答下列问题：

(1)、表中a＝， b＝， c＝；

(2)、补全频数分布直方图．

查看试题解析

19. 已知：如图，在△ABC中，AB＝AC＝5，BC＝8，D，E分别为BC，AB边上一点，∠ADE＝∠C．

(1)、求证：△BDE∽△CAD；

(2)、若CD＝2，求BE的长．

查看试题解析

20. 参照学习函数的过程与方法，探究函数y＝

\frac{x - 2}{x} (x \neq 0)

的图象与性质．

因为y＝ $\frac{x - 2}{x} = 1 - \frac{2}{x}$ ，即y＝﹣ $\frac{2}{x}$ +1，所以我们对比函数y＝﹣ $\frac{2}{x}$ 来探究．

列表：

…

﹣4

﹣3

﹣2

﹣1

﹣ $\frac{1}{2}$

$\frac{1}{2}$

…

y＝﹣ $\frac{2}{x}$

…

$\frac{1}{2}$

$\frac{2}{3}$

﹣4

﹣2

﹣1

﹣ $\frac{2}{3}$

﹣ $\frac{1}{2}$

…

y＝ $\frac{x - 2}{x}$

…

$\frac{3}{2}$

$\frac{5}{3}$

﹣3

﹣1

$\frac{1}{3}$

$\frac{1}{2}$

…

描点：在平面直角坐标系中，以自变量x的取值为横坐标，以y＝ $\frac{x - 2}{x}$ 相应的函数值为纵坐标，描出相应的点，如图所示：

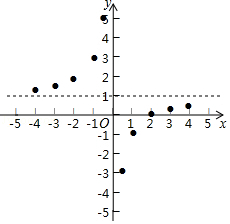(1)、请把y轴左边各点和右边各点，分别用一条光滑曲线顺次连接起来；

(2)、观察图象并分析表格，回答下列问题：

①当x＜0时，y随x的增大而；（填“增大”或“减小”）

②y＝ $\frac{x - 2}{x}$ 的图象是由y＝﹣ $\frac{2}{x}$ 的图象向平移个单位而得到；

③图象关于点中心对称．（填点的坐标）

(3)、设A（x₁ ， y₁），B（x₂ ， y₂）是函数y＝

\frac{x - 2}{x}

的图象上的两点，且x₁+x₂＝0，试求y₁+y₂+3的值．

查看试题解析

21. 如图，四边形ABCD中，AD∥BC，BD⊥DC，∠C＝45°，BD平分∠ABC．

(1)、求证：AB⊥BC；

(2)、已知AD＝AB＝4，BC＝8，点P，Q分别是线段AD，BC上的点，BQ＝2AP，过点P作PR∥AB交BD于R，记y表示△PRQ的面积，x表示线段AP的长度．如果在一个直角三角形中，它的两个锐角都是45°，那么它的两条直角边的长度相等，请你根据题目条件，写出表示变量y与x关系的关系式．

(3)、当x＝时，s取得最大值．

查看试题解析
22. 如图，抛物线y＝ax²+ $\frac{3}{2}$ x+c（a≠0）与x轴交于点A，B两点，其中A（﹣1，0），与y轴交于点C（0，2）．

(1)、求抛物线的表达式及点B坐标；

(2)、点E是线段BC上的任意一点（点E与B、C不重合），过点E作平行于y轴的直线交抛物线于点F，交x轴于点G．
①设点E的横坐标为m，用含有m的代数式表示线段EF的长；

②线段EF长的最大值是．

查看试题解析
23. 如图，在△ABC中，BA＝BC＝20cm，AC＝30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x秒．

(1)、当x为何值时，PQ∥BC；

(2)、是否存在某一时刻，使△APQ∽△CQB？若存在，求出此时AP的长；若不存在，请说理由；

(3)、当CQ＝10时，求 $\frac{S_{△ A P Q}}{S_{△ A B Q}}$ 的值．

查看试题解析