浙江省杭州市2019年中考数学预测卷2
试卷更新日期:2019-04-26 类型:中考模拟
一、选择题(每题3分,共30分)
-
1. 当a=-1 时,(-a2)3 的结果是( )A、-1 B、1 C、a6 D、以上答案都不对2. 清明小长假是广大游客走出家门放松心情、感受祖国大好河山的好时机,为丰富游客出行体验,小长假前夕,遵义市启动了2018年“醉美遵义,四季主题游”之春季踏青赏花游。三天假期,遵义市共接待游客230.11万人次,实现旅游综合收入12.66亿元,把12.66亿用科学记数法表示为( )A、 B、 C、 D、3. 如图,△ABC中,DE∥BC, = ,则OE:OB=( )
 A、 B、 C、 D、4. 若|a|=7,b的相反数是2,则a+b的值()A、-9 B、-9或+9 C、+5或-5 D、+5或-95. 随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2017年底某市汽车拥有量为16.9万辆.已知2015年底该市汽车拥有量为10万辆,设2015年底至2017年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )A、10(1+x)2=16.9 B、10(1+2x)=16.9 C、10(1﹣x)2=16.9 D、10(1﹣2x)=16.96. 下列各式去括号正确的是( )A、a-(b-c)=a-b-c B、a +(b-c)=a+b-c C、 D、7. 如果不等式(a+1)x>a+1的解集为x<1,则a必须满足( )A、a<0 B、a≤1 C、a>-1 D、a<-18. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
A、 B、 C、 D、4. 若|a|=7,b的相反数是2,则a+b的值()A、-9 B、-9或+9 C、+5或-5 D、+5或-95. 随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2017年底某市汽车拥有量为16.9万辆.已知2015年底该市汽车拥有量为10万辆,设2015年底至2017年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )A、10(1+x)2=16.9 B、10(1+2x)=16.9 C、10(1﹣x)2=16.9 D、10(1﹣2x)=16.96. 下列各式去括号正确的是( )A、a-(b-c)=a-b-c B、a +(b-c)=a+b-c C、 D、7. 如果不等式(a+1)x>a+1的解集为x<1,则a必须满足( )A、a<0 B、a≤1 C、a>-1 D、a<-18. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( ) A、 B、 C、 D、9. 如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0,②2a﹣b=0,③a+b+c<0;④c﹣a=3,其中正确的有( )个.
A、 B、 C、 D、9. 如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0,②2a﹣b=0,③a+b+c<0;④c﹣a=3,其中正确的有( )个.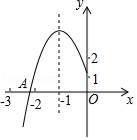 A、1 B、2 C、3 D、410. 如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
A、1 B、2 C、3 D、410. 如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )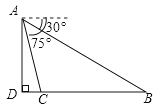 A、300(+1)m B、1200(﹣1)m C、1800(﹣1)m D、2400(﹣1)m
A、300(+1)m B、1200(﹣1)m C、1800(﹣1)m D、2400(﹣1)m二、填空题(每题4分,共240分)
-
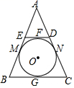
11. 一组数据-1,1,0,5,-3的极差是 .12. 如图所示, 内切△ABC ,切点分别为 , , , 切 于 点,交 , 于点 , ,若△ABC 的周长为12,BC=2,则△ADE 的周长是 .
 13. 现有三张分别画有正三角形、平行四边形、菱形图案的卡片,它们除图案外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的每一张卡片的图案既是轴对称图形又是中心对称图形的概率是 .14. 若 |m|= ,则m= .
13. 现有三张分别画有正三角形、平行四边形、菱形图案的卡片,它们除图案外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的每一张卡片的图案既是轴对称图形又是中心对称图形的概率是 .14. 若 |m|= ,则m= .
15. 如图,DE⊥AB 于 ,AF⊥BC 于 ,若 , ,则 = . 16. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点,已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m,当m=3时,则点B的横坐标是 .
16. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点,已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m,当m=3时,则点B的横坐标是 .
三、解答题(7小题,共66分)
-
17. 在某中学开展的“我为四川地震灾区献爱心”捐书活动中,校团委为了了解九年级同学的捐书情况,用简单的随机抽样方法从九年级的10个班中抽取50名同学,对这50名同学所捐的书进行分类统计后,绘制了如下统计表:

 (1)、在图中,补全这50名同学捐书情况的频数分布直方图;(2)、若九年级共有475名同学,请你估计九年级同学的捐书总册数及学辅类书的册数.
(1)、在图中,补全这50名同学捐书情况的频数分布直方图;(2)、若九年级共有475名同学,请你估计九年级同学的捐书总册数及学辅类书的册数.捐书情况统计表
种类
文学类
科普类
学辅类
体育类
其它
合计
册数
120
180
140
80
40
560
18. 如图,一次函数y=﹣ x+m与x轴、y轴分别交于A、B两点,与正比例函数y=kx交于点C(1, ). (1)、求k、m的值;(2)、求△OAC的面积.19. 如图, 与 有公共顶点 , .
(1)、求k、m的值;(2)、求△OAC的面积.19. 如图, 与 有公共顶点 , . (1)、请你写一个适当的条件,使 ,则需添加的条件可以是或 , 并选择其中之一证明.(2)、由(1)能否得出其他的相似三角形?如果能,请说明理由.20. 如图是某电脑公司 年的销售额 (万元)关于时间 (月)之间的函数图象,其中前几个月两变量之间满足反比例函数关系,后几个月两变量之间满足一次函数关系,观察图象,回答下列问题:
(1)、请你写一个适当的条件,使 ,则需添加的条件可以是或 , 并选择其中之一证明.(2)、由(1)能否得出其他的相似三角形?如果能,请说明理由.20. 如图是某电脑公司 年的销售额 (万元)关于时间 (月)之间的函数图象,其中前几个月两变量之间满足反比例函数关系,后几个月两变量之间满足一次函数关系,观察图象,回答下列问题: (1)、该年度月份的销售额最低;(2)、求出该年度最低的销售额;(3)、若电脑公司月销售额不大于 万元,则称销售处于淡季.在 年中,该电脑公司哪几个月销售处于淡季?21. 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC,AE延长线的交点,AG与CD相交于点F.
(1)、该年度月份的销售额最低;(2)、求出该年度最低的销售额;(3)、若电脑公司月销售额不大于 万元,则称销售处于淡季.在 年中,该电脑公司哪几个月销售处于淡季?21. 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC,AE延长线的交点,AG与CD相交于点F.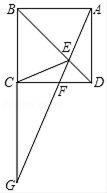 (1)、求证:四边形ABCD是正方形;(2)、当AE=3EF,DF=1时,求GF的值.
(1)、求证:四边形ABCD是正方形;(2)、当AE=3EF,DF=1时,求GF的值.

