浙江省杭州市2019年中考数学预测卷1
试卷更新日期:2019-04-26 类型:中考模拟
一、选择题(共30分)
-
1. 下列计算正确的是( )A、 =±4 B、± =3 C、 =﹣3 D、( )2=32. 如图,已知AB∥CD,AC与BD交于点O,则下列比例中成立的是( )
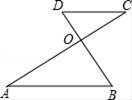 A、 B、 C、 D、3.
A、 B、 C、 D、3.如图所示的几何体的左视图是( )
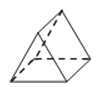 A、
A、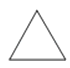 B、
B、 C、
C、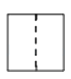 D、
D、 4. 为筹备班级的初中毕业联欢会, 班长对全班同学爱吃哪几种水果作民意调查, 从而最终决定买什么水果。下列调查数据中最值得关注的是( )A、平均数 B、中位数 C、众数 D、方差5. 一列匀速前进的火车,从它进入500 m的隧道到离开,共需30秒,又知在隧道顶部的一盏固定的灯发出的一束光线垂直照射火车5秒,则这列火车的长度是( )A、 m B、100 m C、120 m D、150 m6. 已知矩形的面积为10,则它的长与宽之间的函数关系用图象大致可表示为( )A、
4. 为筹备班级的初中毕业联欢会, 班长对全班同学爱吃哪几种水果作民意调查, 从而最终决定买什么水果。下列调查数据中最值得关注的是( )A、平均数 B、中位数 C、众数 D、方差5. 一列匀速前进的火车,从它进入500 m的隧道到离开,共需30秒,又知在隧道顶部的一盏固定的灯发出的一束光线垂直照射火车5秒,则这列火车的长度是( )A、 m B、100 m C、120 m D、150 m6. 已知矩形的面积为10,则它的长与宽之间的函数关系用图象大致可表示为( )A、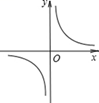 B、
B、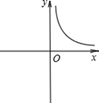 C、
C、 D、
D、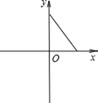 7. 如图, 是⊙O 的直径, 是⊙O 的切线, 为切点, ,则 等于( )
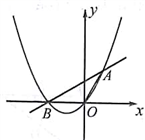
7. 如图, 是⊙O 的直径, 是⊙O 的切线, 为切点, ,则 等于( )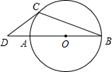 A、25° B、50° C、30° D、40°8. 在Rt△ABC中,∠ACB=90°,AB=10cm,AB边上的高为4cm,则Rt△ABC的周长为( )cm.A、24 B、6 C、3 +10 D、6 +109. 已知a为有理数,定义运算符号▽:当a>-2时,▽a=-a;当a<-2时,▽a=a;当a=-2时,▽a=0.根据这种运算,计算▽[4+▽(2-5)]的值为( )A、-7 B、7 C、-1 D、110. 在平面直角坐标系 中,直线 ( 为常数)与抛物线 交于 , 两点,且 点在 轴左侧, 点坐标为 ,连结 、 ,有以下说法:
A、25° B、50° C、30° D、40°8. 在Rt△ABC中,∠ACB=90°,AB=10cm,AB边上的高为4cm,则Rt△ABC的周长为( )cm.A、24 B、6 C、3 +10 D、6 +109. 已知a为有理数,定义运算符号▽:当a>-2时,▽a=-a;当a<-2时,▽a=a;当a=-2时,▽a=0.根据这种运算,计算▽[4+▽(2-5)]的值为( )A、-7 B、7 C、-1 D、110. 在平面直角坐标系 中,直线 ( 为常数)与抛物线 交于 , 两点,且 点在 轴左侧, 点坐标为 ,连结 、 ,有以下说法:① ;②当 时, 的值随 的增大而增大;③当 时, ;④ 面积的最小值为 .其中正确的是( )
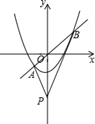 A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题(每题4分,共24分)
-
11.
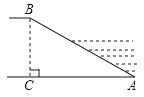
河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1: ,则AB的长为
 12. 一个圆盘被平均分成红、黄、蓝、白、黑5个扇形区域,向其投掷一枚飞镖,且落在圆盘内,则飞镖落在白色区域的概率是 .13. 已知2a-3b2=7,则代数式9b2-6a+4的值是。
12. 一个圆盘被平均分成红、黄、蓝、白、黑5个扇形区域,向其投掷一枚飞镖,且落在圆盘内,则飞镖落在白色区域的概率是 .13. 已知2a-3b2=7,则代数式9b2-6a+4的值是。
14. 已知点P 的坐标满足 ,则点P 关于原点的对称点的坐标为 .15. 如图,在菱形中ABCD,对角线AC、BD相交于点O,E为BC的中点,若菱形的周长为24cm,则OE=cm. 16. 若数a使关于x的不等式组 有且仅有四个整数解,且使关于y的分式方程 =2有非负数解,则满足条件的整数a的值是 .
16. 若数a使关于x的不等式组 有且仅有四个整数解,且使关于y的分式方程 =2有非负数解,则满足条件的整数a的值是 .
三、解答题(66分)
-
17. 下列计算过程对不对,若有错误,请指出原因.
计算:60÷( - + ).
小明的解答:原式=60÷ -60÷ +60÷
=60×4-60×5+60×3
=240-300+180=120;
小强的解答:原式=60÷( - + )
=60÷ =60× = .
18. 甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理过程中,环保部门每月初对两个城市的空气质量进行监测,连续10个月的空气污染指数如下图所示.其中,空气污染指≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.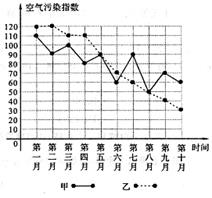 (1)、请填写下表:
(1)、请填写下表:平均数
方差
中位数
空气质量为优的次数
甲
80
1
乙
1060
80
(2)、请回答下面问题:①从平均数和中位数来分析,甲、乙两个城市的空气质量;
②从平均数和方差来分析,甲、乙两个城市的空气质量变化情况;
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.
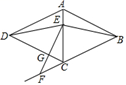
19. 如图,在△ABC中,点D在AB边上,∠ABC=∠ACD,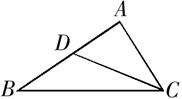 (1)、求证:△ABC∽△ACD(2)、若AD=2,AB=5.求AC的长.20. 一名男生推铅球,铅球行进的高度y(单位:m)与水平距离x(单位:m)之间的关系是 .(1)、铅球行进的最大高度是多少?(2)、该男生把铅球推出的水平距离是多少?(3)、铅球在下落的过程中,行进高度由 m变为 m时,铅球行进的水平距离是多少?21. 如图,正方形 ,点 在 上,将 绕点 顺时针旋转 至 ,点 , 分别为点 , 旋转后的对应点,连接 , , , 与 交于点 , 与 交于点 .
(1)、求证:△ABC∽△ACD(2)、若AD=2,AB=5.求AC的长.20. 一名男生推铅球,铅球行进的高度y(单位:m)与水平距离x(单位:m)之间的关系是 .(1)、铅球行进的最大高度是多少?(2)、该男生把铅球推出的水平距离是多少?(3)、铅球在下落的过程中,行进高度由 m变为 m时,铅球行进的水平距离是多少?21. 如图,正方形 ,点 在 上,将 绕点 顺时针旋转 至 ,点 , 分别为点 , 旋转后的对应点,连接 , , , 与 交于点 , 与 交于点 .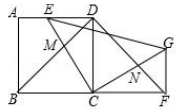 (1)、求证 ;(2)、直接写出图中已经存在的所有等腰直角三角形.
(1)、求证 ;(2)、直接写出图中已经存在的所有等腰直角三角形.