广东省深圳市罗湖区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-04-26 类型:期末考试
一、选择题(共36分)
-
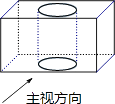
1. 一元二次方程x2+2x=0的根是( )A、x1=0,x2=2 B、x1=0,x2=﹣2 C、x1=1,x2=﹣2 D、x1=1,x2=22. 若点(3,4)是反比例函数y= 图象上一点,此函数图象必须经过点( )A、(2,6) B、(2,﹣6) C、(4,﹣3) D、(3,﹣4)3. 将一个长方体内部挖去一个圆柱(如图所示),它的主视图是( )
 A、
A、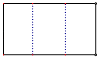 B、
B、 C、
C、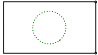 D、
D、 4. 一个菱形的两条对角线的长分别为5和8,那么这个菱形的面积是( )A、40 B、20 C、10 D、255. 二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( )
4. 一个菱形的两条对角线的长分别为5和8,那么这个菱形的面积是( )A、40 B、20 C、10 D、255. 二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( ) A、x1=﹣1,x2=5 B、x1=﹣2,x2=4 C、x1=﹣1,x2=2 D、x1=﹣5,x2=56. 如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A、x1=﹣1,x2=5 B、x1=﹣2,x2=4 C、x1=﹣1,x2=2 D、x1=﹣5,x2=56. 如图,四边形ABCD是平行四边形,下列说法不正确的是( ) A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC⊥BD时,四边形ABCD是菱形 D、当∠DAB=90°时,四边形ABCD是正方形7. 一件衣服的原价是500元,经过两次提价后的价格为621元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )A、500(1+x)2=621 B、500(1﹣x)2=621 C、500(1+x)=621 D、500(1﹣x)=6218. 如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC⊥BD时,四边形ABCD是菱形 D、当∠DAB=90°时,四边形ABCD是正方形7. 一件衣服的原价是500元,经过两次提价后的价格为621元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )A、500(1+x)2=621 B、500(1﹣x)2=621 C、500(1+x)=621 D、500(1﹣x)=6218. 如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )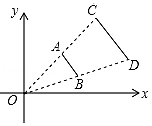 A、(4,4) B、(3,3) C、(3,1) D、(4,1)9. 如图,∠1=∠2,DE∥AC,则图中的相似三角形有( )
A、(4,4) B、(3,3) C、(3,1) D、(4,1)9. 如图,∠1=∠2,DE∥AC,则图中的相似三角形有( )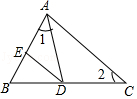 A、2对 B、3对 C、4对 D、5对10. 下列四个函数图象中,当x<0时,函数值y随自变量x的增大而减小的是( )A、
A、2对 B、3对 C、4对 D、5对10. 下列四个函数图象中,当x<0时,函数值y随自变量x的增大而减小的是( )A、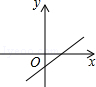 B、
B、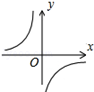 C、
C、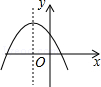 D、
D、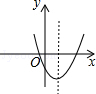 11. 如图,一艘轮船在A处测得灯塔P位于其东北方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )海里.
11. 如图,一艘轮船在A处测得灯塔P位于其东北方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )海里. A、15 +15 B、30 +30 C、45+15 D、6012. 如图,Rt△BOA与Rt△COA的斜边在x轴上,BA=6,A(10,0),AC与OB相交于点E,且CA=CO,连接BC,下列判断一定正确的是( )
A、15 +15 B、30 +30 C、45+15 D、6012. 如图,Rt△BOA与Rt△COA的斜边在x轴上,BA=6,A(10,0),AC与OB相交于点E,且CA=CO,连接BC,下列判断一定正确的是( )①△ABE∽△OCE;②C(5,5);③BC= ;④S△ABC=3.
 A、①③ B、②④ C、①②③ D、①②③④
A、①③ B、②④ C、①②③ D、①②③④二、填空题(共12分)
-
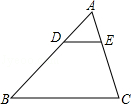
13. 若关于x的一元二次方程x2﹣4x+k=0有两个相等的实数根,则k的值为 .14. 如图,在△ABC中,D、E分别为AB、AC上的点,若DE∥BC, = ,则 = .
 15. 如图,在Rt△ABC中,∠C=90°,AB=4,BC=1,则cosA的值是 .
15. 如图,在Rt△ABC中,∠C=90°,AB=4,BC=1,则cosA的值是 .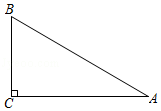 16. 二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:
16. 二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中的x与y的部分对应值如下表:x
﹣1
0
1
3
y
﹣1
3
5
3
当ax2+(b﹣1)x+c>0时,x的取值范围是 .
三、解答题(共52分)
-
17. 计算: cos45°﹣2sin60°+3tan230°﹣(cos60°﹣1)018. 解方程:(x﹣2)2=3(x﹣2).19. 在一个不透明的袋子里有1个红球,1个黄球和n个白球,它们除颜色外其余都相同.(1)、从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于0.5左右,求n的值;(2)、在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.20. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
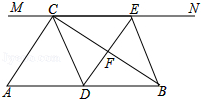 (1)、求证:CE=AD;(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.21. 将一条长为56cm的铁丝剪成两段并把每一段铁丝做成一个正方形.(1)、要使这两个正方形的面积之和等于100cm2 , 该怎么剪?(2)、设这两个正方形的面积之和为Scm2 , 当两段铁丝长度分别为何值时,S有最小值?22. 如图,在矩形OABC中,OA=3,OC=4,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y= (k>0)的图象经过点D且与边BA交于点E,作直线DE.
(1)、求证:CE=AD;(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.21. 将一条长为56cm的铁丝剪成两段并把每一段铁丝做成一个正方形.(1)、要使这两个正方形的面积之和等于100cm2 , 该怎么剪?(2)、设这两个正方形的面积之和为Scm2 , 当两段铁丝长度分别为何值时,S有最小值?22. 如图,在矩形OABC中,OA=3,OC=4,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y= (k>0)的图象经过点D且与边BA交于点E,作直线DE. (1)、当点D运动到BC中点时,求k的值;(2)、求 的值;(3)、连接DA,当△DAE的面积为 时,求k值.23. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+3与直线y=x﹣3交于点A(3,0)和点B(﹣2,n),与y轴交于点C.
(1)、当点D运动到BC中点时,求k的值;(2)、求 的值;(3)、连接DA,当△DAE的面积为 时,求k值.23. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+3与直线y=x﹣3交于点A(3,0)和点B(﹣2,n),与y轴交于点C. (1)、求出抛物线的函数表达式;(2)、在图1中,平移线段AC,点A、C的对应点分别为M、N,当N点落在线段AB上时,M点也恰好在抛物线上,求此时点M的坐标;(3)、如图2,在(2)的条件下,在抛物线上是否存在点P(不与点A重合),使△PMC的面积与△AMC的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、求出抛物线的函数表达式;(2)、在图1中,平移线段AC,点A、C的对应点分别为M、N,当N点落在线段AB上时,M点也恰好在抛物线上,求此时点M的坐标;(3)、如图2,在(2)的条件下,在抛物线上是否存在点P(不与点A重合),使△PMC的面积与△AMC的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.