广东省河源市紫金县2018-2019学年九年级下学期数学学业调研测试试卷
试卷更新日期:2019-04-26 类型:中考模拟
一、选择题(共30分)
-
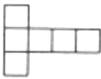
1. 下列各数中,比-2小的数是( )A、2 B、0 C、-1 D、-32. 如图,下图经过折叠不能围成一个正方体是( )A、
 B、
B、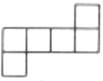 C、
C、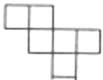 D、
D、 3. 已知数据:2,1,4,6,9,8,6,1.则这组数据的中位数是( )A、4 B、5 C、6 D、4和64. 若⊙O的半径为6,点P在⊙O内,则OP的长可能是( )A、5 B、6 C、7 D、85. 关于x的一元二次方程x2-(k+3)x+k=0的根的情况是( )A、有两不相等实数根 B、有两相等实数根 C、无实数根 D、不能确定6. 已如实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
3. 已知数据:2,1,4,6,9,8,6,1.则这组数据的中位数是( )A、4 B、5 C、6 D、4和64. 若⊙O的半径为6,点P在⊙O内,则OP的长可能是( )A、5 B、6 C、7 D、85. 关于x的一元二次方程x2-(k+3)x+k=0的根的情况是( )A、有两不相等实数根 B、有两相等实数根 C、无实数根 D、不能确定6. 已如实数a,b在数轴上的位置如图所示,下列结论中正确的是( ) A、a>b B、|a|<|b| C、ab>0 D、-a>b7. 函数y= 中自变量x的取值范围是( )A、x≥-3 B、x≠-3 C、x>-3 D、x≤-38. 如图,直线AC和直线BD相交于点0,若∠1+∠2=90°,则∠BOC的度数是( )
A、a>b B、|a|<|b| C、ab>0 D、-a>b7. 函数y= 中自变量x的取值范围是( )A、x≥-3 B、x≠-3 C、x>-3 D、x≤-38. 如图,直线AC和直线BD相交于点0,若∠1+∠2=90°,则∠BOC的度数是( )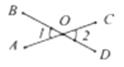 A、100° B、115° C、135° D、145°9. 下列计算正确的是( )A、a2·a3=a6 B、2a+3b=5ab C、a8÷a2=a6 D、(a2b)2=a4b10. 若关于x的一元一次方程2x+3a=1的解为x=2,则关于m的一元一次不等式3-m>a的解集为( )A、m<2 B、m<4 C、m>2 D、m>4
A、100° B、115° C、135° D、145°9. 下列计算正确的是( )A、a2·a3=a6 B、2a+3b=5ab C、a8÷a2=a6 D、(a2b)2=a4b10. 若关于x的一元一次方程2x+3a=1的解为x=2,则关于m的一元一次不等式3-m>a的解集为( )A、m<2 B、m<4 C、m>2 D、m>4二、填空题(共24分)
-
11. 计算: ·cos45°= .12. 某市常住人口约为5240000人,数字5240000用科学记数法表示.13. 如图,AB是半圆的直径,∠BAC=20°,D是 的中点,则∠DAC的度数是.
 14. 如图△ABC中,AC=12,DE为AB的垂直平分线,△BCE的周长为20.则BC的长为.
14. 如图△ABC中,AC=12,DE为AB的垂直平分线,△BCE的周长为20.则BC的长为. 15.
15.已知二次函数y= -x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为。
 16. 如图,在正方形ABCD中,对角线BD的长为 。若将BD绕点B旋转后,点D落在BC延长线上的点D'处,点D经过的路径为弧DD',则图中阴影部分的面积是 .
16. 如图,在正方形ABCD中,对角线BD的长为 。若将BD绕点B旋转后,点D落在BC延长线上的点D'处,点D经过的路径为弧DD',则图中阴影部分的面积是 .
三、解答题(一)(共18分)
-
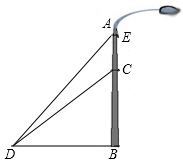
17. 解方程:x2+8x-9=018. 先化简,再求值:(x+2)(x-2)-(x-1)2 , 其中x=- .19. 如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
四、解答题(二)(共21分)
-
20. 某市某幼儿园“六一”期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏。主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.(1)、若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)?(2)、若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少。(画出树状图或列表)21. 某中学校开展了“献爱心”捐款活动。第一天收到捐款10000元,第三天收到捐款12100元。(1)、如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)、按照(1)中收到捐款的增长速度,第四天该校能收到多少捐款?22. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高。

五、解答题(三)(共27分)
-
23. 如图,已知A、B两点的坐标分别为A(0, ),B(2,0),直线AB与反比例函数y= 的图象交于点C和点D(-1,a).
 (1)、求直线AB和反比例函数的解析式;(2)、求∠ACO的度数。
(1)、求直线AB和反比例函数的解析式;(2)、求∠ACO的度数。

