上海市长宁区2019届高三上学期理数期末质量检测一模试卷
试卷更新日期:2019-04-26 类型:高考模拟
一、单选题
-
1. 已知 ,则“ ”是“ ”的( )A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分又非必要条件2. 有一批种子,对于一颗种子来说,它可能 天发芽,也可能 天发芽, ,下表是不同发芽天数的种子数的记录:
发芽天数
1
2
3
4
5
6
7
种子数
8
26
22
24
12
4
2
0
统计每颗种子发芽天数得到一组数据,则这组数据的中位数是( )
A、 B、 C、 D、3. 已知向量 和 的夹角为 ,且 ,则 ( )A、 B、 C、 D、4. 某位喜欢思考的同学在学习函数的性质时提出了如下两个命题:已知函数 的定义域为 , ,① 若当 时,都有 ,则函数 是 上的奇函数;② 若当 时,都有 ,则函数 是 上的增函数.下列判断正确的是( )A、①和②都是真命题 B、①是真命题,②是假命题 C、①和②都是假命题 D、①是假命题,②是真命题二、填空题
-
5. 已知集合 , ,则6. 已知 ,则7. 在 的二项展开式中,常数项为(结果用数值表示)8. 已知向量 , ,若向量 ∥ ,则实数9. 若圆锥的侧面积为 ,底面积为 ,则该圆锥的体积为。
 10. 已知幂函数 的图像过点 ,则 的定义域为11. 已知 ,且 ,则12. 已知函数 和 的图像如图所示,则不等式 的解集是
10. 已知幂函数 的图像过点 ,则 的定义域为11. 已知 ,且 ,则12. 已知函数 和 的图像如图所示,则不等式 的解集是 13. 如图,某学生社团在校园内测量远处某栋楼 的高度, 为楼顶,线段 的长度为 ,在 处测得 ,在 处测得 ,且此时看楼顶 的仰角 ,已知楼底 和 、 在同一水平面上,则此楼高度 (精确到 )
13. 如图,某学生社团在校园内测量远处某栋楼 的高度, 为楼顶,线段 的长度为 ,在 处测得 ,在 处测得 ,且此时看楼顶 的仰角 ,已知楼底 和 、 在同一水平面上,则此楼高度 (精确到 )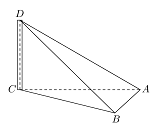 14. 若甲、乙两位同学随机地从 门课程中选修 门,则两人选修的课程中恰有 门相同的概率为.15. 已知数列 的前 项和为 ,且 ,若数列 收敛于常数 ,则首项 取值的集合为16. 已知 、 、 与 、 、 是 个不同的实数,若关于 的方程 的解集 是有限集,则集合 中最多有个元素
14. 若甲、乙两位同学随机地从 门课程中选修 门,则两人选修的课程中恰有 门相同的概率为.15. 已知数列 的前 项和为 ,且 ,若数列 收敛于常数 ,则首项 取值的集合为16. 已知 、 、 与 、 、 是 个不同的实数,若关于 的方程 的解集 是有限集,则集合 中最多有个元素三、解答题
-
17. 求下列不等式的解集:(1)、 ;(2)、18. 《九章算术》中,将底面为长方形且有一条侧棱与地面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马,如图所示,在阳马 中, 底面 .
 (1)、已知 ,斜梁 与底面 所成角为 ,求立柱 的长;(精确到 )(2)、求证:四面体 为鳖臑.19. 已知△ 的三个内角 、 、 所对应的边分别为 、 、 ,复数 , ,(其中 是虚数单位),且 .(1)、求证: ,并求边长 的值;(2)、判断△ 的形状,并求当 时,角 的大小.
(1)、已知 ,斜梁 与底面 所成角为 ,求立柱 的长;(精确到 )(2)、求证:四面体 为鳖臑.19. 已知△ 的三个内角 、 、 所对应的边分别为 、 、 ,复数 , ,(其中 是虚数单位),且 .(1)、求证: ,并求边长 的值;(2)、判断△ 的形状,并求当 时,角 的大小.