2019年广东省中考数学模拟卷1
试卷更新日期:2019-04-25 类型:中考模拟
一、选择题
-
1. -2的相反数是( )A、-2 B、2 C、 D、±22. 据统计,2017年河南省的夏粮收购总产量为796.24亿斤,请用科学记数法表示这个数为( )A、7.9624×1010 B、7.9624×109 C、79.624×109 D、0.79624×10113. 如图,圆柱体中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )
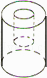 A、
A、 B、
B、 C、
C、 D、
D、 4. 一个袋子中装有3个红球和2个黄球,这些球的形状、大小、质地完全相同,在看不到球的条件下,随机从袋中摸出2个球,其中2个球颜色不相同的概率是( )A、 B、 C、 D、5. 下面的图形中既是轴对称图形又是中心对称图形的是( )A、
4. 一个袋子中装有3个红球和2个黄球,这些球的形状、大小、质地完全相同,在看不到球的条件下,随机从袋中摸出2个球,其中2个球颜色不相同的概率是( )A、 B、 C、 D、5. 下面的图形中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 某同学做了四道题:①3m+4n=7mn;②(﹣2a2)3=﹣8a6;③6x6÷2x2=3x3;④y3•xy2=xy5 , 其中正确的题号是( )A、②④ B、①③ C、①② D、③④7. 如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
6. 某同学做了四道题:①3m+4n=7mn;②(﹣2a2)3=﹣8a6;③6x6÷2x2=3x3;④y3•xy2=xy5 , 其中正确的题号是( )A、②④ B、①③ C、①② D、③④7. 如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( ) A、100° B、90° C、80° D、70°8. 如图,双曲线y= (x>0)经过线段AB的中点M,则△AOB的面积为( )
A、100° B、90° C、80° D、70°8. 如图,双曲线y= (x>0)经过线段AB的中点M,则△AOB的面积为( )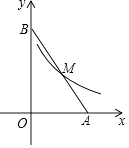 A、18 B、24 C、6 D、129. 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )
A、18 B、24 C、6 D、129. 如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为( )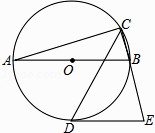 A、 B、2 C、2 D、310. 如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
A、 B、2 C、2 D、310. 如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )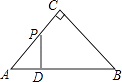 A、
A、 B、
B、 C、
C、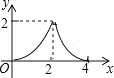 D、
D、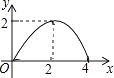
二、填空题
-
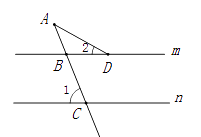
11. 分解因式:ma2﹣4ma+4m= .12. 若关于x的一元二次方程x2+2x﹣k=0没有实数根,则k的取值范围是 .13. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等
 14. 如图,在平行四边形ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF∶CF= .
14. 如图,在平行四边形ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF∶CF= .
15. 如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE=时,△EGH为等腰三角形.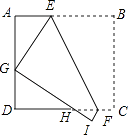 16. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作 交AB于点E,以点B为圆心,BC的长为半径作交AB于点D,则阴影部分的面积为 .
16. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作 交AB于点E,以点B为圆心,BC的长为半径作交AB于点D,则阴影部分的面积为 .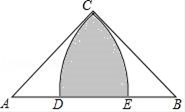
三、解答题(一)
-
17. 计算:( )﹣2+(π﹣2014)0+sin60°+| ﹣2|.18. 先化简,再求值:
,其中a满足 .
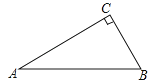
19.如图,在△ABC中,∠C=90°.
(1)用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连结BD,若BD平分∠CBA,求∠A的度数.
四、解答题(二)
-
20. 甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)、求乙骑自行车的速度;(2)、当甲到达学校时,乙同学离学校还有多远?21. 某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了以下两幅不完整的统计图:
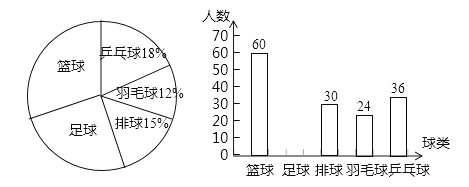
请根据以上统计图提供的信息,解答下列问题:
(1)共抽取多少名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“篮球”所对应的圆心角的度数;
(3)该校共有2500名学生,请估计全校学生喜欢足球运动的人数.
22. 如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据 ≈1.41, ≈1.73).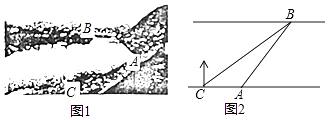
五、解答题(三)
-
23. 如图,直线L: 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动。
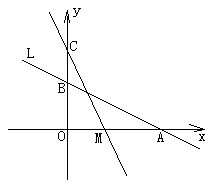 (1)、求A、B两点的坐标;(2)、求△COM的面积S与M的移动时间t之间的函数关系式;(3)、当t为何值时△COM≌△AOB,并求此时M点的坐标。24. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)、求A、B两点的坐标;(2)、求△COM的面积S与M的移动时间t之间的函数关系式;(3)、当t为何值时△COM≌△AOB,并求此时M点的坐标。24. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.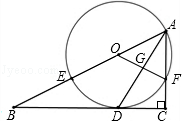 (1)、求证:BC是⊙O的切线;(2)、设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;(3)、若BE=8,sinB= ,求DG的长,25. 如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)、求证:BC是⊙O的切线;(2)、设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;(3)、若BE=8,sinB= ,求DG的长,25. 如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.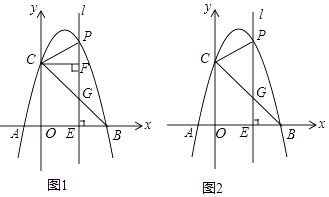 (1)、求抛物线的表达式;(2)、当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)、如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
(1)、求抛物线的表达式;(2)、当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)、如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.