广东省中山市2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-04-24 类型:期末考试
一、单项选择题(满分30分)
-
1. 下列是电视台的台标,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知点A(2,3)在双曲线y= 上,则下列哪个点也在该双曲线上( )A、(﹣1,6) B、(6,﹣1) C、(﹣2,﹣3) D、(﹣2,3)3. 天气预报说“中山市明天降水概率是20%”,理解正确的是( )A、中山市明天将有20%的地区降水 B、中山市明天降水的可能性较小 C、中山市明天将有20%的时间降水 D、中山市明天降水的可能性较大4. 用配方法解方程x2﹣4x=0,下列配方正确的是( )A、(x+2)2=0 B、(x﹣2)2=0 C、(x+2)2=4 D、(x﹣2)2=45. 抛物线y=3x2向右平移一个单位得到的抛物线是( )A、y=3x2+1 B、y=3x2﹣1 C、y=3(x+1)2 D、y=3(x﹣1)26. 如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则下列各点中在⊙A外的是( )
2. 已知点A(2,3)在双曲线y= 上,则下列哪个点也在该双曲线上( )A、(﹣1,6) B、(6,﹣1) C、(﹣2,﹣3) D、(﹣2,3)3. 天气预报说“中山市明天降水概率是20%”,理解正确的是( )A、中山市明天将有20%的地区降水 B、中山市明天降水的可能性较小 C、中山市明天将有20%的时间降水 D、中山市明天降水的可能性较大4. 用配方法解方程x2﹣4x=0,下列配方正确的是( )A、(x+2)2=0 B、(x﹣2)2=0 C、(x+2)2=4 D、(x﹣2)2=45. 抛物线y=3x2向右平移一个单位得到的抛物线是( )A、y=3x2+1 B、y=3x2﹣1 C、y=3(x+1)2 D、y=3(x﹣1)26. 如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则下列各点中在⊙A外的是( )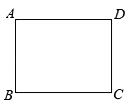 A、点A B、点B C、点C D、点D7. 对于二次函数y= (x﹣2)2+1的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线x=﹣2 C、顶点坐标是(2,1) D、与x轴有两个交点8. 如图,△ABC内接于⊙O,CD是⊙O的直径,∠BCD=54°,则∠A的度数是( )
A、点A B、点B C、点C D、点D7. 对于二次函数y= (x﹣2)2+1的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线x=﹣2 C、顶点坐标是(2,1) D、与x轴有两个交点8. 如图,△ABC内接于⊙O,CD是⊙O的直径,∠BCD=54°,则∠A的度数是( ) A、36° B、33° C、30° D、27°9. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
A、36° B、33° C、30° D、27°9. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )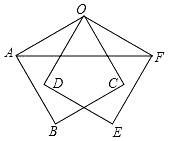 A、20° B、25° C、30° D、35°10. 函数y= 与y=kx2﹣k(k≠0)在同一直角坐标系中的图象可能是( )A、
A、20° B、25° C、30° D、35°10. 函数y= 与y=kx2﹣k(k≠0)在同一直角坐标系中的图象可能是( )A、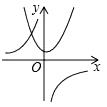 B、
B、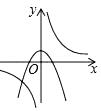 C、
C、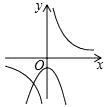 D、
D、
二、填空题(满分24分)
-
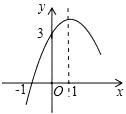
11. 点(2,3)关于原点对称的点的坐标是 .12. 已知a是关于x的一元二次方程2x2+x﹣2=0的一个根,则4a2+2a+3= .13. 在一个不透明的布袋中装有红色、黄色的球共40个,除颜色外其它完全相同.通过多次摸球试验后发现摸到黄色球的频率稳定在25%左右,则口袋中黄色球可能有个.14. 二次函数的部分图象如图所示,则使y>0的x的取值范围是 .
 15. 如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y= (x<0)的图象经过点C,则k的值为 .
15. 如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y= (x<0)的图象经过点C,则k的值为 .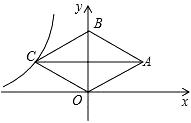 16. 如图,将半径为2,圆心角为90°的扇形BAC绕点A逆时针旋转60°,点B、C的对应点分别为D、E,点D在 上,则阴影部分的面积为 .
16. 如图,将半径为2,圆心角为90°的扇形BAC绕点A逆时针旋转60°,点B、C的对应点分别为D、E,点D在 上,则阴影部分的面积为 .
三、解答题(一)(满分18分)
-
17. 解方程:x2﹣3x﹣1=0.18. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
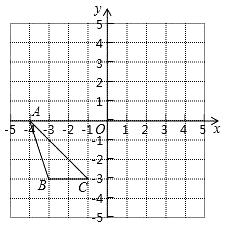 (1)、画出△ABC绕点O顺时针旋转90°后的△A′B′C′.(2)、求点B绕点O旋转到点B′的路径长(结果保留π).19. 已知x2﹣4x+1﹣m=0是关于x的一元二次方程.(1)、若x=4是方程的一个实数根,求m的值;(2)、若该方程有两个不相等的实数根,求m的取值范围.
(1)、画出△ABC绕点O顺时针旋转90°后的△A′B′C′.(2)、求点B绕点O旋转到点B′的路径长(结果保留π).19. 已知x2﹣4x+1﹣m=0是关于x的一元二次方程.(1)、若x=4是方程的一个实数根,求m的值;(2)、若该方程有两个不相等的实数根,求m的取值范围.四、解答题(二)(满分21分)
-
20. 某学校自主开发了A书法、B阅读,C绘画,D器乐四门选修课程供学生选择,每门课程被选到的机会均等.(1)、若学生小玲计划选修两门课程,请写出她所有可能的选法;(2)、若学生小强和小明各计划选修一门课程,则他们两人恰好选修同一门课程的概率为多少?21. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,弦PB与CD交于点F,且FC=FB.
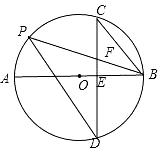 (1)、求证:PD∥CB;(2)、若AB=26,EB=8,求CD的长度.22. 某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=﹣2x+200.为保证市场稳定,供货商规定销售价格不得低于75元/件.(1)、写出每天的销售利润w(元)与销售价格x(元)的函数关系式(不必写出x的取值范围);(2)、每件小电器的销售价格定为多少元时,才能使该款小电器每天获得的利润是1200元?
(1)、求证:PD∥CB;(2)、若AB=26,EB=8,求CD的长度.22. 某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=﹣2x+200.为保证市场稳定,供货商规定销售价格不得低于75元/件.(1)、写出每天的销售利润w(元)与销售价格x(元)的函数关系式(不必写出x的取值范围);(2)、每件小电器的销售价格定为多少元时,才能使该款小电器每天获得的利润是1200元?五、解答题(三)(满分27分)
-
23. 如图,在平面直角坐标系中,一次函数y=﹣2x+b的图象与反比例函数y= 的图象交于点A(1,n)、B(﹣2,2).
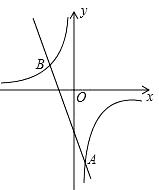 (1)、求k、n、b的值;(2)、若x轴正半轴上有一点M,满足△MAB的面积为12,求点M的坐标.24. 已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)、求k、n、b的值;(2)、若x轴正半轴上有一点M,满足△MAB的面积为12,求点M的坐标.24. 已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.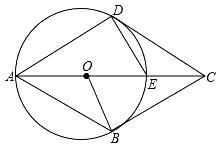 (1)、求证:DE=OE;(2)、若CD∥AB,求证:BC是⊙O的切线;(3)、在(2)的条件下,求证:四边形ABCD是菱形.25. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)、求证:DE=OE;(2)、若CD∥AB,求证:BC是⊙O的切线;(3)、在(2)的条件下,求证:四边形ABCD是菱形.25. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).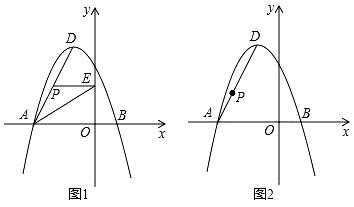 (1)、求抛物线的函数解析式,并写出顶点D的坐标;(2)、如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;(3)、如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
(1)、求抛物线的函数解析式,并写出顶点D的坐标;(2)、如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;(3)、如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.