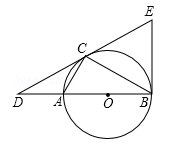
广东省汕头市潮南区两英镇2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-04-24 类型:期末考试
一、选择题(共30分)
-
1. 下列方程是关于 的一元二次方程的是A、 B、 C、 D、2. 如图图形中,既是轴对称图形,又是中心对称图形的是A、
 B、
B、 C、
C、 D、
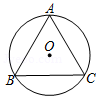
D、 3. 将抛物线 向左平移2个单位后得到新的抛物线的表达式为A、 B、 C、 D、4. 如图,四边形ABCD为 的内接四边形,∠BCD=120°,则∠BOD的大小是( )
3. 将抛物线 向左平移2个单位后得到新的抛物线的表达式为A、 B、 C、 D、4. 如图,四边形ABCD为 的内接四边形,∠BCD=120°,则∠BOD的大小是( )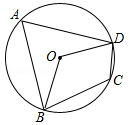
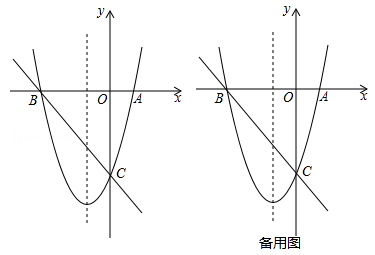
A、 B、 C、 D、5. 边长为2的正方形内接于 ,则 的半径是A、1 B、2 C、 D、6. 方程 的左边配成完全平方后所得方程为A、 B、 C、 D、7. A,B是 上的两点, , 的长是 ,则 的度数是A、30 B、 C、 D、8. 某种植基地2017年蔬菜产量为80吨,预计2019年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为 ,则可列方程为A、 B、 C、 D、9. 如图,将 绕点 逆时针旋转 ,得到 .若点 在线段 的延长线上,则 的大小为 A、 B、 C、 D、10. 如图,抛物线 的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示,下列结论:
A、 B、 C、 D、10. 如图,抛物线 的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示,下列结论:① ②方程 的两个根是 , ③ ④当 时, 随 增大而增大.其中正确的个数是
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(共24分)
-
11. 若 是方程 的根,计算: .12. 已知一个圆锥的底面直径为 ,母线长 ,则这个圆锥的表面积是(结果保留)13. 一个不透明盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是 .14. 若 是等边 的外接圆, 的半径为2,则等边 的边长为 .
 15. 抛物线y=x2+2x+1的顶点坐标是 .16. 已知正方形 中,点 在边 上, , (如图所示)把线段 绕点 旋转,使点 落在直线 上的点 处,则 、 两点的距离为 .
15. 抛物线y=x2+2x+1的顶点坐标是 .16. 已知正方形 中,点 在边 上, , (如图所示)把线段 绕点 旋转,使点 落在直线 上的点 处,则 、 两点的距离为 .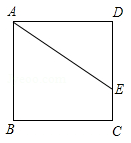
三、解答题(共18分)
-
17. 已知 是关于 的方程 的一个根,求 的值.18. 设二次函数的图象的顶点坐标为 ,且过点 ,求这个函数的关系式.19. 在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系 是格点三角形(顶点在网格线的交点上)
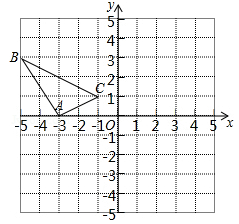 (1)、先作 关于原点 成中心对称的△ ,再把△ 向上平移4个单位长度得到△ ;(2)、△ 与 是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
(1)、先作 关于原点 成中心对称的△ ,再把△ 向上平移4个单位长度得到△ ;(2)、△ 与 是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.四、解答题(共21分)
-
20. 小明、小林是三河中学九年级的同班同学,在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并将被编入A、B、C三个班,他俩希望能再次成为同班同学.(1)、请你用画树状图法或列举法,列出所有可能的结果;(2)、求两人再次成为同班同学的概率.21. 如图,在 中, , , 是 边上一点(点 与 , 不重合),连结 ,将线段 绕点 按逆时针方向旋转 得到线段 ,连结 交 于点 ,连接 .
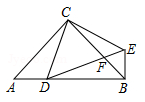 (1)、求证: ;(2)、当 时,求 的度数.22. 已知关于 的方程 .(1)、若方程总有两个实数根,求 的取值范围;(2)、若两实数根 、 满足 ,求 的值.
(1)、求证: ;(2)、当 时,求 的度数.22. 已知关于 的方程 .(1)、若方程总有两个实数根,求 的取值范围;(2)、若两实数根 、 满足 ,求 的值.五、解答题(共27分)
-
23. 2016年3月国际风筝节在铜仁市万山区举办,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:(1)、用表达式表示蝙蝠型风筝销售量 (个 与售价 (元 之间的函数关系 ;(2)、王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?(3)、当售价定为多少时,王大伯获得利润最大,最大利润是多少?