2013年广西来宾市中考数学试卷

试卷更新日期：2017-05-12 类型：中考真卷

进入出卷网下载

一、选择题.

1. ﹣3的绝对值是（　　）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2.
如图是由六个大小相同的小正方体组成的几何体，它的主视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 分解因式：x²﹣4y²的结果是（　　）

A、（x+4y）（x﹣4y） B、（x+2y）（x﹣2y） C、（x﹣4y）² D、（x﹣2y）²

查看试题解析
4. 下列式子计算正确的是（　　）

A、x+x²=x³ B、3x²﹣2x=x C、（3x²y）²=3x⁴y² D、（﹣3x²y）²=9x⁴y²

查看试题解析
5. 2013年全国参加高考的人数为9120000人，这个数字用科学记数法表示是（　　）

A、91.2×10⁵ B、9.12×10⁶ C、9.12×10⁷ D、0.912×10⁷

查看试题解析
6.
如图，直线AB∥CD，∠CGF=130°，则∠BFE的度数是（　　）

A、30° B、40° C、50° D、60°

查看试题解析
7. 已知图形：①等边三角形，②平行四边形，③菱形，④圆．其中既是轴对称图形，又是中心对称图形的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知反比例函数的图象经过点（2，﹣1），则它的解析式是（　　）

A、y=﹣2x B、y=2x C、 $y = \frac{2}{x}$ D、 $y = - \frac{2}{x}$

查看试题解析
9. 已知关于x的一元二次方程x²﹣x+k=0的一个根是2，则k的值是（　　）

A、﹣2 B、2 C、1 D、﹣1

查看试题解析
10. 已知数据：10，17，13，8，11，13．这组数据的中位数和极差分别是（　　）

A、12和9 B、12和8 C、10.5和9 D、13和8

查看试题解析
11.
如图，AB=AC，D，E分别是AB，AC上的点，下列条件中不能证明△ABE≌△ACD的是（　　）

A、AD=AE B、BD=CE C、BE=CD D、∠B=∠C

查看试题解析
12.
如图，其图象反映的过程是：张强从家去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家，其中x表示时间，y表示张强离家的距离．根据图象，下列回答正确的是（　　）

A、张强在体育场锻炼45分钟 B、张强家距离体育场是4千米 C、张强从离家到回到家一共用了200分钟 D、张强从家到体育场的平均速度是10千米/小时

查看试题解析

二、填空题

13. $\sqrt{5}$ 的相反数是．

查看试题解析
14. 从1，2，3这三个数字中任意抽取两个，其和是偶数的概率是．

查看试题解析
15. 不等式组 ${\begin{cases} x - 3 \geq 0 \\ 2 x > 8 \end{cases}$ 的解集是．

查看试题解析
16. 在△ABC中，∠C=90°，BC=6， $\sin A = \frac{2}{3}$ ，则AB边的长是．

查看试题解析
17.
如图是一圆形水管的截面图，已知⊙O的半径OA=13，水面宽AB=24，则水的深度CD是．

查看试题解析
18. 已知二次函数y=x²+bx+c经过点（3，0）和（4，0），则这个二次函数的解析式是．

查看试题解析

三、解答题：

19.

(1)、计算： ${(1 - π)}^{0} + {(- 1)}^{2013} + {(\frac{1}{2})}^{- 1} - \sqrt{9}$

(2)、解方程： $\frac{2}{x + 2} = \frac{1}{2 x}$ ．

查看试题解析
20.
如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（0，3），B（﹣3，5），C（﹣4，1）．
①把△ABC向右平移2个单位得△A₁B₁C₁ ，请画出△A₁B₁C₁ ，并写出点A₁的坐标；
②把△ABC绕原点O旋转180°得到△A₂B₂C₂ ，请画出△A₂B₂C₂ ．

查看试题解析
21.
某校九年级为建立学习兴趣小组，对语文、数学、英语、物理、化学、思想品德、历史、综合共八个科目的喜欢情况进行问卷调查（每人只选一项），下表是随机抽取部分学生的问卷进行统计的结果：
科目
语文
数学
英语
物理
化学
思想品德
历史
综合
人数
6
10
11
12
10
9
8
14
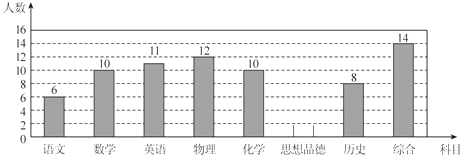
根据表中信息，解答下列问题：

(1)、本次随机抽查的学生共有人；

(2)、本次随机抽查的学生中，喜欢科目的人数最多；

(3)、根据上表中的数据补全条形统计图；

(4)、如果该校九年级有600名学生，那么估计该校九年级喜欢综合科目的学生有多少人．

查看试题解析
22. 某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．

(1)、降价前商场每月销售该商品的利润是多少元？

(2)、要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？

查看试题解析
23.
如图，在等腰梯形ABCD中，AD∥BC，E，F，G，H分别是梯形各边的中点．

(1)、请用全等符号表示出图中所有的全等三角形（不得添加辅助线），并选其中一对加以证明；

(2)、求证：四边形EFGH是菱形．

查看试题解析
24.
如图，A，B，C，D是⊙O上的四点，∠BAC=∠CAD，P是线段CD延长线上一点，且∠PAD=∠ABD．

(1)、请判断△BCD的形状（不要求证明）；

(2)、求证：PA是⊙O的切线；

(3)、求证：AP²﹣DP²=DP•BC．

查看试题解析
25.
在△AOB中，∠AOB=90°，AO=6厘米，BO=8厘米，分别以OB和OA所在直线为x轴，y轴建立平面直角坐标系，如图所示，动点M从点A开始沿AO方向以2厘米/秒的速度向点O移动，同时动点N从点O开始沿OB方向以4厘米/秒的速度向点B移动（其中一点到达终点时，另一点随即停止移动）．

(1)、求过点A和点B的直线表达式；

(2)、当点M移动多长时间时，四边形AMNB的面积最小？并求出四边形AMNB面积的最小值；

(3)、在点M和点N移动的过程中，是否存在以O，M，N为顶点的三角形与△AOB相似？若存在，请求出点M 和点N的坐标；若不存在，请说明理由．

查看试题解析

科目	语文	数学	英语	物理	化学	思想品德	历史	综合
人数	6	10	11	12	10	9	8	14