2013年广西桂林市中考数学试卷

试卷更新日期：2017-05-12 类型：中考真卷

进入出卷网下载

一、选择题.

1. 下面各数是负数的是（　　）

A、0 B、﹣2013 C、|﹣2013| D、 $\frac{1}{2013}$

查看试题解析
2. 在 0，2，﹣2， $\frac{2}{3}$ 这四个数中，最大的数是（　　）

A、2 B、0 C、﹣2 D、 $\frac{2}{3}$

查看试题解析
3.
如图，与∠1是同位角的是（　　）

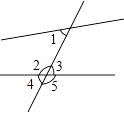A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
4. 下列运算正确的是（　　）

A、5²•5³=5⁶ B、（5²）³=5⁵ C、5²÷5³=5 D、（ $\sqrt{5}$ ）²=5

查看试题解析
5. 7位同学中考体育测试立定跳远成绩（单位：分）分别是：8，9，7，6，10，8，9，这组数据的中位数是（　　）

A、6 B、8 C、9 D、10

查看试题解析
6. 下列物体的主视图、俯视图和左视图不全是圆的是（　　）

A、橄榄球 B、乒乓球 C、篮球 D、排球

查看试题解析
7. 不等式x+1＞2x﹣4的解集是（　　）

A、x＜5 B、x＞5 C、x＜1 D、x＞1

查看试题解析
8. 下列图形中既是中心对称图形又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
9. 下列命题的逆命题不正确的是（　　）

A、平行四边形的对角线互相平分 B、两直线平行，内错角相等 C、等腰三角形的两个底角相等 D、对顶角相等

查看试题解析
10.
如图，菱形ABCD的对角线BD、AC分别为2、2 $\sqrt{3}$ ，以B为圆心的弧与AD、DC相切，则阴影部分的面积是（　　）

A、2 $\sqrt{3}$ ﹣ $\frac{\sqrt{3}}{3}$ π B、4 $\sqrt{3}$ ﹣ $\frac{\sqrt{3}}{3}$ π C、4 $\sqrt{3}$ ﹣π D、2 $\sqrt{3} - π$

查看试题解析
11. 已知关于x的一元二次方程x²+2x+a﹣1=0有两根为x₁和x₂ ，且x₁²﹣x₁x₂=0，则a的值是（　　）

A、a=1 B、a=1或a=﹣2 C、a=2 D、a=1或a=2

查看试题解析
12.
如图，已知边长为4的正方形ABCD，P是BC边上一动点（与B、C不重合），连结AP，作PE⊥AP交∠BCD的外角平分线于E．设BP=x，△PCE面积为y，则y与x的函数关系式是（　　）

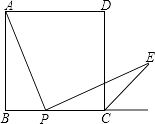A、y=2x+1 B、y= $\frac{1}{2}$ x﹣2x² C、y=2x﹣ $\frac{1}{2}$ x² D、y=2x

查看试题解析

二、填空题.

13. 分解因式：3ab²﹣a²b= ．

查看试题解析
14. 我国雾霾天气多发，PM2.5颗粒物被称为大气的元凶．PM2.5是指直径小于或等于2.5微米的颗粒物，已知1毫米=1000微米，用科学记数法表示2.5微米是毫米．

查看试题解析
15. 桂林市某气象站测得六月份一周七天的降雨量分别为0，32，11，45，8，51，27（单位：mm），这组数据的极差是．

查看试题解析
16.
如图，在△ABC中，CA=CB，AD⊥BC，BE⊥AC，AB=5，AD=4，则AE= ．

查看试题解析
17.
函数y=x的图象与函数y= $\frac{4}{x}$ 的图象在第一象限内交于点B，点C是函数y= $\frac{4}{x}$ 在第一象限图象上的一个动点，当△OBC的面积为3时，点C的横坐标是．

查看试题解析
18.
如图，已知线段AB=10，AC=BD=2，点P是CD上一动点，分别以AP、PB为边向上、向下作正方形APEF和PHKB，设正方形对角线的交点分别为O₁、O₂ ，当点P从点C运动到点D时，线段O₁O₂中点G的运动路径的长是．

查看试题解析

三、解答题．

19. 计算：（1﹣ $\sqrt{3}$ ）⁰﹣ $\sqrt{12}$ +2sin60°﹣|﹣ $\sqrt{3}$ |

查看试题解析
20. 解二元一次方程组： ${\begin{cases} 3 x + 2 y = 19 \\ 2 x - y = 1 \end{cases}$ ．

查看试题解析
21.
如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连接AF，DE交于点O．求证：

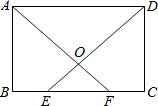(1)、△ABF≌△DCE；

(2)、△AOD是等腰三角形．

查看试题解析
22. 在重阳节敬老爱老活动中，某校计划组织志愿者服务小组到“夕阳红”敬老院为老人服务，准备从初三（1）班中的3名男生小亮、小明、小伟和2名女生小丽、小敏中选取一名男生和一名女生参加学校志愿者服务小组．

(1)、若随机选取一名男生和一名女生参加志愿者服务小组，请用树状图或列表法写出所有可能出现的结果；

(2)、求出恰好选中男生小明与女生小丽的概率．

查看试题解析
23. 在“美丽广西，清洁乡村”活动中，李家村村长提出了两种购买垃圾桶方案；方案1：买分类垃圾桶，需要费用3000元，以后每月的垃圾处理费用250元；方案2：买不分类垃圾桶，需要费用1000元，以后每月的垃圾处理费用500元；设方案1的购买费和每月垃圾处理费共为y₁元，交费时间为x个月；方案2的购买费和每月垃圾处理费共为y₂元，交费时间为x个月．

(1)、直接写出y₁、y₂与x的函数关系式；

(2)、
在同一坐标系内，画出函数y₁、y₂的图象；

(3)、在垃圾桶使用寿命相同的情况下，哪种方案省钱？

查看试题解析
24. 水源村在今年退耕还林活动中，计划植树200亩，全村在完成植树40亩后，某环保组织加入村民植树活动，并且该环保组织植树的速度是全村植树速度的1.5倍，整个植树过程共用了13天完成．

(1)、全村每天植树多少亩？

(2)、如果全村植树每天需2000元工钱，环保组织是义务植树，因此实际工钱比计划节约多少元？

查看试题解析
25.
如图，在△ABC中，∠C=90°，∠BAC的平分线AD交BC于D，过点D作DE⊥AD交AB于E，以AE为直径作⊙O．

(1)、求证：点D在⊙O上；

(2)、求证：BC是⊙O的切线；

(3)、若AC=6，BC=8，求△BDE的面积．

查看试题解析
26.
已知抛物线的顶点为（0，4）且与x轴交于（﹣2，0），（2，0）．

(1)、直接写出抛物线解析式；

(2)、如图，将抛物线向右平移k个单位，设平移后抛物线的顶点为D，与x轴的交点为A、B，与原抛物线的交点为P．
①当直线OD与以AB为直径的圆相切于E时，求此时k的值；
②是否存在这样的k值，使得点O、P、D三点恰好在同一条直线上？若存在，求出k值；若不存在，请说明理由．

查看试题解析