2013年广西贵港市中考数学试卷

试卷更新日期：2017-05-12 类型：中考真卷

进入出卷网下载

一、选择题.

1. ﹣3的绝对值是（）

A、﹣ $\frac{1}{3}$ B、 $\frac{1}{3}$ C、﹣3 D、3

查看试题解析
2. 纳米是非常小的长度单位，1纳米=10^﹣9米^.。某种病菌的长度约为50纳米，用科学记数法表示该病菌的长度，结果正确的是（）

A、5×10^﹣10米 B、5×10^﹣9米 C、5×10^﹣8米 D、5×10^﹣7米

查看试题解析
3. 下列四种调查：
①调查某班学生的身高情况；
②调查某城市的空气质量；
③调查某风景区全年的游客流量；
④调查某批汽车的抗撞击能力．
其中适合用全面调查方式的是（　　）

A、① B、② C、③ D、④

查看试题解析
4. 下列四个式子中，x的取值范围为x≥2的是（　　）

A、 $\frac{\sqrt{x - 2}}{x - 2}$ B、 $\frac{1}{\sqrt{x - 2}}$ C、 $\sqrt{x - 2}$ D、 $\sqrt{2 - x}$

查看试题解析
5. 下列计算结果正确的是（　　）

A、3a﹣（﹣a）=2a B、a³×（﹣a）²=a⁵ C、a⁵÷a=a⁵ D、（﹣a²）³=a⁶

查看试题解析
6.
如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“共”字一面的相对面上的字是（　　）

A、美 B、丽 C、家 D、园

查看试题解析
7. 下列四个命题中，属于真命题的是（　　）

A、若 $\sqrt{a^{2}}$ =m，则a=m B、若a＞b，则am＞bm C、两个等腰三角形必定相似 D、位似图形一定是相似图形

查看试题解析
8. 关于x的分式方程 $\frac{m}{x + 1} = - 1$ 的解是负数，则m的取值范围是（　　）

A、m＞﹣1 B、m＞﹣1且m≠0 C、m≥﹣1 D、m≥﹣1且m≠0

查看试题解析
9.
如图，直线a∥b，直线c与a、b都相交，从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角，则所选取的两个角互为补角的概率是（　　）

A、 $\frac{3}{5}$ B、 $\frac{2}{5}$ C、 $\frac{1}{5}$ D、 $\frac{2}{3}$

查看试题解析
10.
如图，已知圆锥的母线长为6，圆锥的高与母线所夹的角为θ，且sinθ= $\frac{1}{3}$ ，则该圆锥的侧面积是（　　）

A、24 $\sqrt{2} π$ B、24π C、16π D、12π

查看试题解析
11.
如图，点A（a，1）、B（﹣1，b）都在双曲线y=﹣ $\frac{3}{x} (x < 0)$ 上，点P、Q分别是x轴、y轴上的动点，当四边形PABQ的周长取最小值时，PQ所在直线的解析式是（　　）

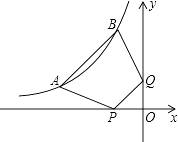A、y=x B、y=x+1 C、y=x+2 D、y=x+3

查看试题解析
12.
如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F，将△DEF沿EF折叠，点D恰好落在BE上M点处，延长BC、EF交于点N．有下列四个结论：
①DF=CF；
②BF⊥EN；
③△BEN是等边三角形；
④S_△_BEF=3S_△_DEF ．
其中，将正确结论的序号全部选对的是（　　）

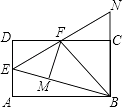A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

二、填空题

13. 若超出标准质量0.05克记作+0.05克，则低于标准质量0.03克记作克．

查看试题解析
14. 分解因式：3x²﹣18x+27= ．

查看试题解析
15. 若一组数据1，7，8，a，4的平均数是5、中位数是m、极差是n，则m+n= ．

查看试题解析
16.
如图，AB是⊙O的弦，OH⊥AB于点H，点P是优弧上一点，若AB=2 $\sqrt{3}$ ，OH=1，则∠APB的度数是．

查看试题解析
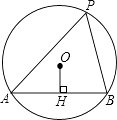17.
如图，△ABC和△FPQ均是等边三角形，点D、E、F分别是△ABC三边的中点，点P在AB边上，连接EF、QE．若AB=6，PB=1，则QE= ．

查看试题解析
18.
如图，在平面直角坐标系xOy中，若动点P在抛物线y=ax²上，⊙P恒过点F（0，n），且与直线y=﹣n始终保持相切，则n=（用含a的代数式表示）．

查看试题解析

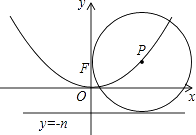
三、解答题

19.

(1)、计算： $\sqrt{9} - {(\frac{1}{2})}^{- 1} + {(2 - \sqrt{2})}^{0}$ ﹣2cos60°；

(2)、先化简：（ $\frac{1}{x + 1} - 1$ ） $\div \frac{x}{x^{2} - 1}$ ，再选择一个恰当的x值代入求值．

查看试题解析
20.
如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3）、B（﹣3，1）、C（﹣1，3）．

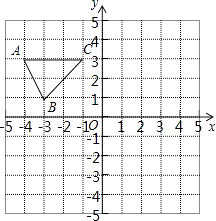(1)、请按下列要求画图：
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度，得到△A₁B₁C₁ ，画出△A₁B₁C₁；
②△A₂B₂C₂与△ABC关于原点O成中心对称，画出△A₂B₂C₂ ．

(2)、在（1）中所得的△A₁B₁C₁和△A₂B₂C₂关于点M成中心对称，请直接写出对称中心M点的坐标．

查看试题解析
21.
如图，在平面直角坐标系xOy中，△ABC的边AC在x轴上，边BC⊥x轴，双曲线y= $\frac{k}{x} (x > 0)$ 与边BC交于点D（4，m），与边AB交于点E（2，n）．

(1)、求n关于m的函数关系式；

(2)、若BD=2，tan∠BAC= $\frac{1}{2}$ ，求k的值和点B的坐标．

查看试题解析
22.
在以“关爱学生、安全第一”为主题的安全教育宣传月活动中，某学校为了了解本校学生的上学方式，在全校范围内随机抽查部分学生，了解到上学方式主要有：A﹣结伴步行、B﹣自行乘车、C﹣家人接送、D﹣其他方式，并将收集的数据整理绘制成如下两幅不完整的统计图．请根据图中信息，解答下列问题：

(1)、本次抽查的学生人数是多少人？

(2)、请补全条形统计图；

(3)、请补全扇形统计图，并在图中标出“自行乘车”对应扇形的圆心角的度数；

(4)、如果该校学生有2080人，请你估计该校“家人接送”上学的学生约有多少人？

查看试题解析
23.
如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG．

(1)、求证：四边形DEGF是平行四边形；

(2)、当点G是BC的中点时，求证：四边形DEGF是菱形．

查看试题解析
24. 在校园文化建设中，某学校原计划按每班5幅订购了“名人字画”共90幅．由于新学期班数增加，决定从阅览室中取若干幅“名人字画”一起分发，如果每班分4幅，则剩下17幅；如果每班分5幅，则最后一班不足3幅，但不少于1幅．

(1)、该校原有的班数是多少个？

(2)、新学期所增加的班数是多少个？

查看试题解析
25.
如图，在边长为2的正方形ABCD中，以点D为圆心、DC为半径作 $\hat{A C}$ ，点E在AB上，且与A、B两点均不重合，点M在AD上，且ME=MD，过点E作EF⊥ME，交BC于点F，连接DE、MF．

(1)、求证：EF是 $\hat{A C}$ 所在⊙D的切线；

(2)、当MA= $\frac{3}{4}$ 时，求MF的长；

(3)、试探究：△MFE能否是等腰直角三角形？若是，请直接写出MF的长度；若不是，请说明理由．

查看试题解析
26.
如图，在平面直角坐标系xOy中，抛物线y=ax²+bx+c交y轴于点C（0，4），对称轴x=2与x轴交于点D，顶点为M，且DM=OC+OD．

(1)、求该抛物线的解析式；

(2)、设点P（x，y）是第一象限内该抛物线上的一个动点，△PCD的面积为S，求S关于x的函数关系式，并写出自变量x的取值范围；

(3)、在（2）的条件下，若经过点P的直线PE与y轴交于点E，是否存在以O、P、E为顶点的三角形与△OPD全等？若存在，请求出直线PE的解析式；若不存在，请说明理由．

查看试题解析