广东省江门市江海区六校联考2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-04-23 类型：期末考试
一、选择题（共30分）
-
1. 如图四个图案中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 如果线段a，b，c能组成三角形，那么它们的长度比可能是（ ）A、1：2：4 B、2：3：4 C、3：4：7 D、1：3：43. 石墨烯是现在世界上最薄的纳米材料，其理论厚度仅是0.00000000034m，这个数用科学记数法表示正确的是（ ）A、3.4×10﹣9 B、0.34×10﹣9 C、3.4×10﹣10 D、3.4×10﹣114. 下列运算中，正确的是（ ）A、a•a2=a2 B、（a2）2=a4 C、a2•a3=a6 D、（a2b）3=a2•b35. 如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD＝2，则点P到边OA的距离是（ ）
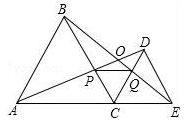
A、1 B、2 C、 D、46. 如果分式 有意义，则x的取值范围是（ ）A、x＝﹣3 B、x＞﹣3 C、x≠﹣3 D、x＜﹣37. 如图，在△ABC中，∠A＝80°，∠C＝60°，则外角∠ABD的度数是（ ）
A、100° B、120° C、140° D、160°8. 下列各式是完全平方式的是（ ）A、x2﹣x+ B、1+x2 C、x+xy+1 D、x2+2x﹣19. 一个多边形内角和是1080°，则这个多边形是（ ）A、六边形 B、七边形 C、八边形 D、九边形10. 如图所示，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下四个结论：①△ACD≌△BCE；②AD＝BE；③∠AOB＝60°；④△CPQ是等边三角形．其中正确的是（ ）
A、①②③④ B、②③④ C、①③④ D、①②③二、填空题（共24分）
-
11. 点A（﹣2，1）关于y轴对称的点的坐标为 ．12. 一个多边形的每个内角都等于150°，则这个多边形是边形．13. 分解因式：x3y﹣4xy= ．14. 如图，△ABC≌△DCB，A、B的对应顶点分别为点D、C，如果AB＝6cm，BC＝12cm，AC＝10cm，DO＝3cm，那么OC的长是cm．
15. 在△ABC中，AB＝AC，AB的垂直平分线交AC于D，交AB于E，连接BD，若∠ADE＝40°，则∠DBC＝ ．
16. 已知a+ =3，则a2+ 的值是 ．三、解答题一（共18分）
-
17. 解方程： ＝1﹣18. 先化简，再求值：（3x+2）（3x﹣2）﹣10x（x﹣1）+（x﹣1）2 ， 其中x＝﹣1．19. 作图题：在∠AOB内有两点M、N，求作一点P使得PM＝PN，且P到∠AOB两边的距离相等．要求尺规作图，不写作法，保留作图痕迹．
四、解答题二（共21分）
-
20. 如图，直线EF∥GH，点A在EF上，AC交GH于点B，若∠EAB＝110°，∠C＝60°，点D在GH上，求∠BDC的度数．
21. 甲、乙两工程队共同完成一项工程，乙队先单独做1天后，再由甲、乙两队合作2天就完成了全部工程，已知甲队单独完成这项工程所需的天数是乙队单独完成工程所需天数的2倍，则甲、乙两单独完成工程各需多少天？22. 如图：已知AB＝AC＝AD，且AD∥BC.求证：∠C＝2∠D．
五、解答题三（共27分）
-
23. 如图，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．
(1)、求证：AE＝CD；(2)、若AC＝12cm，求BD的长．24. 潮州旅游文化节开幕前，某凤凰茶叶公司预测今年凤凰茶叶能够畅销，就用32000元购进了一批凤凰茶叶，上市后很快脱销，茶叶公司又用68000元购进第二批凤凰茶叶，所购数量是第一批购进数量的2倍，但每千克凤凰茶叶进价多了10元．(1)、该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克？(2)、如果这两批茶叶每千克的售价相同，且全部售完后总利润率不低于20%，那么每千克售价至少是多少元？25. 如图所示，已知△ABC中，AB＝AC＝10厘米，BC＝8厘米，点D为AB的中点．如果点P在线段BC上以1厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动．
(1)、若点Q与点P的运动速度相等，经过3秒后，△BPD与△CQP是否全等？请说明理由；(2)、若点Q与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？