2012年广西钦州市中考数学试卷

试卷更新日期：2017-05-12 类型：中考真卷

进入出卷网下载

一、选择题.

1. 下列各数中，是负数的是（　　）

A、﹣2 B、0 C、0.3 D、 $\sqrt{5}$

查看试题解析
2. 下列四幅图案中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列说法错误的是（　　）

A、两点之间线段最短 B、对顶角相等 C、为了了解生产的一批炮弹的杀伤半径，适宜采用全面调查的方式 D、“通常加热到100℃时，水沸腾”这个事情属于必然事件

查看试题解析
4. 如图是由4个小正方体组成的立体图形，它的主视图是（　　）

A、 B、 C、 D、

查看试题解析
5. 黄岩岛是我国的固有领土，这段时间，中菲黄岩岛事件成了各大新闻网站的热点话题．某天，小芳在“百度”搜索引擎中输入“黄岩岛事件最新进展”，能搜索到相关结果约7050000个，7050000这个数用科学记数法表示为（　　）

A、7.05×10⁵ B、7.05×10⁶ C、0.705×10⁶ D、0.705×10⁷

查看试题解析
6. 估算 $\sqrt{17} + 1$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
7. 图中两个四边形是位似图形，它们的位似中心是（　　）

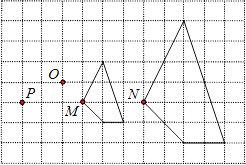A、点M B、点N C、点O D、点P

查看试题解析
8. 下列运算正确的是（　　）

A、2a²﹣a²=2 B、2a•3a=6a² C、（a﹣b）²=a²﹣b² D、a⁶÷a²=a³

查看试题解析
9. 不等式组 ${\begin{cases} x + 2 > 0 \\ 2 x - 3 \leq 1 \end{cases}$ 的解集在数轴上表示正确的是（　　）

A、 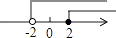B、 C、 D、

查看试题解析
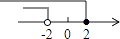10. 如图所示，把一张矩形纸片对折，折痕为AB，再把以AB的中点O为顶点的平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开平铺后得到的平面图形一定是（　　）

A、正三角形 B、正方形 C、正五边形 D、正六边形

查看试题解析
11. 如果把 $\frac{5 x}{x + y}$ 的x与y都扩大10倍，那么这个代数式的值（　　）

A、不变 B、扩大50倍 C、扩大10倍 D、缩小到原来的 $\frac{1}{10}$

查看试题解析
12. 在平面直角坐标系中，对于平面内任意一点（x，y），若规定以下两种变换：
①f（x，y）=（y，x）．如f（2，3）=（3，2）；
②g（x，y）=（﹣x，﹣y），如g（2，3）=（﹣2，﹣3）．
按照以上变换有：f（g（2，3））=f（﹣2，﹣3）=（﹣3，﹣2），那么g（f（﹣6，7））等于（）

A、（7，6） B、（7，﹣6） C、（﹣7，6） D、（﹣7，﹣6）

查看试题解析

二、填空题.

13. 6的相反数是．

查看试题解析
14. 分解因式：x²﹣4= ．

查看试题解析
15. 已知等腰三角形的顶角为80°，那么它的一个底角为．

查看试题解析
16. 某班共有50名同学，其中有2名同学习惯用左手写字，其余同学都习惯用右手写字，老师随机请1名同学到黑板板演，习惯用左手写字的同学被选中的概率是．

查看试题解析
17. 如图，在等腰梯形ABCD中，AB∥CD，AC⊥BC，∠B=60°，BC=8，则等腰梯形ABCD的周长为．

查看试题解析
18.
如图，直线y=﹣ $\frac{3}{2}$ x+3与x轴、y轴分别交于A、B两点，把△AOB绕点A旋转90°后得到△AO′B′，则点B′的坐标是．

查看试题解析

三、解答题。

19. 计算：2^﹣¹+|﹣3|﹣ $\sqrt{9}$ +（π﹣3）⁰ ．

查看试题解析
20. 如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，求证：AB=DC．

查看试题解析
21. 如图，已知正比例函数y=3x的图象与反比例函数y= $\frac{k}{x}$ 的图象交于点A（1，m）和点B．

(1)、求m的值和反比例函数的解析式．

(2)、观察图象，直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围．

查看试题解析
22. 6月5日是世界环境日，某校组织了一次环保知识竞赛，每班选25名同学参加比赛，成绩分别为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将某年级的一班和二班的成绩整理并绘制成统计图：
根据以上提供的信息解答下列问题：

(1)、把一班竞赛成绩统计图补充完整；

(2)、写出下表中a、b、c的值：
平均数（分）
中位数（分）
众数（分）
一班
a
b
90
二班
87.6
80
c

(3)、请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析：
①从平均数和中位数方面比较一班和二班的成绩；②从平均数和众数方面比较一班和二班的成绩；③从B级以上（包括B级）的人数方面来比较一班和二班的成绩．

查看试题解析
23. 近年来，某县为发展教育事业，加大了对教育经费的投入，2009年投入6000万元，2011年投入8640万元．

(1)、求2009年至2011年该县投入教育经费的年平均增长率；

(2)、该县预计2012年投入教育经费不低于9500万元，若继续保持前两年的平均增长率，该目标能否实现？请通过计算说明理由．

查看试题解析
24.
如图所示，小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度，测得电梯楼顶部B处的仰角为45°，底部C处的俯角为26°，已知小明家楼房的高度AD=15米，求电梯楼的高度BC（结果精确到0.1米）（参考数据：sin26°≈0.44，cos26°≈0.90，tan26°≈0.49）

查看试题解析
25. 如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC．

(1)、求证：EF是⊙O的切线；

(2)、求证：AC²=AD•AB；

(3)、若⊙O的半径为2，∠ACD=30°，求图中阴影部分的面积．

查看试题解析
26.
如图甲，在平面直角坐标系中，A、B的坐标分别为（4，0）、（0，3），抛物线y= $\frac{3}{4}$ x²+bx+c经过点B，且对称轴是直线x=﹣ $\frac{5}{2}$ ．

(1)、求抛物线对应的函数解析式；

(2)、将图甲中△ABO沿x轴向左平移到△DCE（如图乙），当四边形ABCD是菱形时，请说明点C和点D都在该抛物线上；

(3)、在（2）中，若点M是抛物线上的一个动点（点M不与点C、D重合），经过点M作MN∥y轴交直线CD于N，设点M的横坐标为t，MN的长度为l，求l与t之间的函数解析式，并求当t为何值时，以M、N、C、E为顶点的四边形是平行四边形．（参考公式：抛物线y=ax²+bx+c（a≠0）的顶点坐标为（﹣ $\frac{b}{2 a}$ ， $\frac{4 a c - b^{2}}{4 a}$ ），对称轴是直线x=﹣ $\frac{b}{2 a}$ ．）

查看试题解析

	平均数（分）	中位数（分）	众数（分）
一班	a	b	90
二班	87.6	80	c