2012年广西来宾市中考数学试卷
试卷更新日期：2017-05-12 类型：中考真卷
一、选择题
-
1. 如图，已知几何体由5个相同的小正方体组成，那么它的主视图是（ ）
A、
B、
C、
D、
2. 在下列平面图形中，是中心对称图形的是（ ）A、
B、
C、
D、
3. 如果2x2y3与x2yn+1是同类项，那么n的值是（ ）A、1 B、2 C、3 D、44. 如图，在△ABC中，已知∠A=80°，∠B=60°，DE∥BC，那么∠CED的大小是（ ）
A、40° B、60° C、120° D、140°5. 在平面直角坐标系中，将点M（1，2）向左平移2个长度单位后得到点N，则点N的坐标是（ ）
A、（﹣1，2） B、（3，2） C、（1，4） D、（1，0）6. 分式方程 的解是（ ）A、x=﹣2 B、x=1 C、x=2 D、x=37. 在一个不透明的袋子中，装有形状、质地、大小等完全相同的1个黑球、2个白球、3个黄球、4个红球．从中随机抽取一个，那么取出的小球是黄球的概率是（ ）A、 B、 C、 D、8. 已知关于x的一元二次方程x2+x+m=0的一个实数根为1，那么它的另一个实数根是（ ）A、﹣2 B、0 C、1 D、29. 已知三组数据：①2，3，4；②3，4，5；③1， ，2．分别以每组数据中的三个数为三角形的三边长，构成直角三角形的有（ ）A、② B、①② C、①③ D、②③10. 下列运算正确的是（ ）A、6a﹣（2a﹣3b）=4a﹣3b B、（ab2）3=ab6 C、2x3•3x2=6x5 D、（﹣c）4÷（﹣c）2=﹣c211. 使式子 有意义的x的取值范围是（ ）A、x≥﹣1 B、﹣1≤x≤2 C、x≤2 D、﹣1＜x＜212. 如图，已知线段OA交⊙O于点B，且OB=AB，点P是⊙O上的一个动点，那么∠OAP的最大值是（ ）
A、30° B、45° C、60° D、90°二、填空题
-
13. 数据组：26，28，25，24，28，26，28的众数是 ．14. 分解因式：2xy﹣4x2= ．15. 如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转100°得到△OA1B1 ， 则∠A1OB=°．
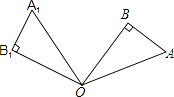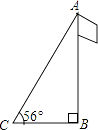
16. 请写出一个图象在第二、第四象限的反比例函数解析式，你所写的函数解析式是 ．17. 已知等腰三角形的一个内角是80°，则它的底角是°．18.如图，为测量旗杆AB的高度，在与B距离为8米的C处测得旗杆顶端A的仰角为56°，那么旗杆的高度约是米（结果保留整数）．（参考数据：sin56°≈0.829，cos56°≈0.559，tan56°≈1.483）
三、解答题
-
19. 计算(1)、计算：π0+2﹣1﹣ ﹣|﹣ |；(2)、 ，其中x=4，y=﹣2．20. 某数学兴趣小组在本校九年级学生中以“你最喜欢的一项体育运动”为主题进行了抽样调查，并将调查结果绘制成如图图表：
项目
篮球
乒乓球
羽毛球
跳绳
其他
人数
a
12
10
5
8
请根据图表中的信息完成下列各题：
(1)、本次共调查学生名；(2)、a= ， 表格中五个数据的中位数是；(3)、在扇形图中，“跳绳”对应的扇形圆心角是；(4)、如果该年级有450名学生，那么据此估计大约有人最喜欢“乒乓球”．21. 有甲、乙两种车辆参加来宾市“桂中水城”建设工程挖渠运土，已知5辆甲种车和4辆乙种车一次可运土共140立方米，3辆甲种车和2辆乙种车一次可运土共76立方米．求甲、乙两种车每辆一次可分别运土多少立方米？22. 如图，在▱ABCD中，BE交对角线AC于点E，DF∥BE交AC于点F．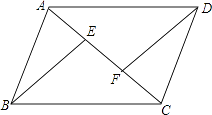
(1)、写出图中所有的全等三角形（不得添加辅助线）；(2)、求证：BE=DF．23. 已知点A（6，0）及在第一象限的动点P（x，y），且2x+y=8，设△OAP的面积为S．(1)、试用x表示y，并写出x的取值范围；(2)、求S关于x的函数解析式；(3)、△OAP的面积是否能够达到30？为什么？
