2012年广西贺州市中考数学试卷

试卷更新日期：2017-05-12 类型：中考真卷

进入出卷网下载

一、选择题：

1. $\sqrt[3]{8}$ 等于（　　）

A、4 B、﹣2 C、±2 D、2

查看试题解析
2. 某校为了了解1200名学生的视力情况，从中抽取了300名学生进行视力调查，在这个问题中，下列说法错误的是（　　）

A、总体是1200名学生的视力情况 B、样本是300名学生的视力情况 C、样本容量是300名 D、个体是每名学生的视力情况

查看试题解析
3. 分式方程 $\frac{2}{x - 3} = \frac{12}{x^{2} - 9}$ 的解是（　　）

A、3 B、﹣3 C、±3 D、无解

查看试题解析
4. 如图，AB是⊙O的直径，CD是弦，AB⊥CD，垂足为点E，连接OD、CB、AC，∠DOB=60°，EB=2，那么CD的长为（　　）

A、 $\sqrt{3}$ B、2 $\sqrt{3}$ C、3 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
5. 由一些相同的小正方体搭成的几何体的三视图如图所示，则搭成该几何体的小正方体有（　　）

A、3个 B、4个 C、5个 D、6个

查看试题解析
6. 已知一组数据：3，4，5，6，5，7．那么这组数据的方差是（　　）

A、 $\frac{5}{3}$ B、 $\frac{1}{2}$ C、 $\frac{4}{3}$ D、 $\frac{2}{3}$

查看试题解析
7. 如图，在▱ABCD中，E为AD的三等分点，AE= $\frac{2}{3}$ AD，连接BE交AC于点F，AC=12，则AF为（　　）

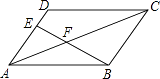A、4 B、4.8 C、5.2 D、6

查看试题解析
8. 已知反比例函数 $y = \frac{k}{x}$ ，在每一个象限内y随x的增大而增大，点A在这个反比例函数图象上，AB⊥x轴，垂足为点B，△ABO的面积为9，那么反比例函数的解析式为（　　）

A、 $y = - \frac{18}{x}$ B、 $y = \frac{18}{x}$ C、 $y = \frac{9}{x}$ D、 $y = - \frac{9}{x}$

查看试题解析
9. 在一个不透明的布袋里装有4个小球，其中2个红球，1个白球，1个黄球，它们除颜色外其它完全相同．那么一次性摸出两个小球恰好都是红球的概率是（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
10. 已知一次函数y=kx﹣k与反比例函数 $y = \frac{k}{x}$ 在同一直角坐标系中的大致图象是（　　）

A、 B、 C、 D、

查看试题解析
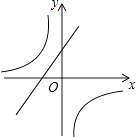11. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列结论：
①4a﹣b＜0；
②abc＜0；
③a+b+c＜0；
④a﹣b+c＞0；
⑤4a+2b+c＞0．
其中错误的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，正方形ABCD和EFGC中，正方形EFGC的边长为a，用a的代数式表示阴影部分△AEG的面积为（　　）

A、 $\frac{3}{2} a^{2}$ B、 $\frac{2}{3} a^{2}$ C、 $\frac{1}{2} a^{2}$ D、a²

查看试题解析

二、填空题

13. ﹣5的相反数是．

查看试题解析
14. 使函数 $y = \frac{3}{\sqrt{3 x + 1}}$ 有意义的自变量x的取值范围是．

查看试题解析
15. 微电子技术的不断进步，使半导体材料的精加工尺寸大幅度缩小．某种电子元件的面积大约为0.00000053平方毫米，用科学记数法表示为平方毫米．

查看试题解析
16. 因式分解：3a³﹣6a²b+3ab²= ．

查看试题解析
17. 已知 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ 是关于x，y的二元一次方程组 ${\begin{cases} 2 a x - b y = 3 \\ a x + b y = 6 \end{cases}$ 的解，则a+b= ．

查看试题解析
18. 如图，在菱形ABCD中，边AB的垂直平分线与对角线AC相交于点E，∠ABC=140°，那么∠EDC= ．

查看试题解析
19. 如图一小虫从P点出发绕边长为10cm的等边三角形ABC爬行一圈回到点P，在小虫爬行过程中，始终保持与三角形ABC的边的距离是2cm，求小虫爬过的路径的长是．

查看试题解析
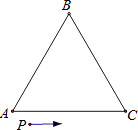20. 如图，已知△ABC的AC边在直线m上，∠ACB=80°，以C为圆心， $\frac{1}{2}$ BC长为半径画弧，交直线m于点D₁、交BC于点E₁ ，连接D₁E₁；又以D₁为圆心， $\frac{1}{2}$ D₁E₁长为半径画弧，交直线m于点D₂、交D₁E₁于点E₂ ，连接D₂E₂；又以D₂为圆心， $\frac{1}{2}$ D₂E₂长为半径画弧，交直线m于点D₃、交D₂E₂于点E₃ ，连接D₃E₃；如此依次下去，…，第n次时所得的∠E_nD_nD_n_﹣₁= ．

查看试题解析

三、解答题：

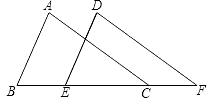
21.

(1)、计算：|﹣2012|+（3.14﹣π）⁰+sin30°﹣2^﹣¹

(2)、先化简，再求值： $\frac{x + 1}{x + 3} + \frac{3 - x}{x} \div \frac{x^{2} - 9}{x^{2}}$ ，其中 $x = \sqrt{2} - 3$ ．

查看试题解析
22. 已知：如图，AB∥DE，AC∥DF，BE=CF，AB=3cm．求DE的长．

查看试题解析
23.
如图，△ABC的三个顶点都在格点上，每个小方格边长均为1个单位长度，建立如图坐标系．

(1)、请你作出△ABC关于点A成中心对称的△AB₁C₁（其中B的对称点是B₁ ， C的对称点是C₁），并写出点B₁、C₁的坐标．

(2)、依次连接BC₁、C₁B₁、B₁C．猜想四边形BC₁B₁C是什么特殊四边形？并说明理由．

查看试题解析
24.
随着科学技术的不断进步，我国海上能源开发和利用已达到国际领先水平．下图为我国在南海海域自主研制的海上能源开发的机器装置AB，一直升飞机在离海平面l距离为150米的空中点P处，看到该机器顶部点A处的俯角为38°，看到露出海平面的机器部分点B处的俯角为65°，求这个机器装置露出海平面部分AB的高度？（结果精确到0.1，参考数据：sin65°=0.9063，sin38°=0.6157，tan38°=0.7813，tan65°=2.1445．）

查看试题解析
25. 如图是我市交警在一个路口统计的某个时段来往车辆的车速情况．（单位：千米/时）

(1)、计算这些车的平均速度．

(2)、大多数车以哪一个速度行驶？

(3)、中间的车速是多少？

查看试题解析
26. 某生物实验室需培育一群有益菌．现有60个活体样本，经过两轮培植后，总和达24000个，其中每个有益菌每一次可分裂出若干个相同数目的有益菌．

(1)、每轮分裂中平均每个有益菌可分裂出多少个有益菌？

(2)、按照这样的分裂速度，经过三轮培植后有多少个有益菌？

查看试题解析
27. 如图，P为⊙O外一点，PA、PB为⊙O的切线，A、B为切点，AC为⊙O的直径，PO交于⊙O于点E．

(1)、试判断∠APB与∠BAC的数量关系；

(2)、若⊙O的半径为4，P是⊙O外一动点，是否存在点P，使四边形PAOB为正方形？若存在，请求出PO的长，并判断点P的个数及其满足的条件；若不存在，请说明理由．

查看试题解析
28.
如图，抛物线 $y = \frac{1}{2} x^{2} + \frac{3}{2} x + 2$ 与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，连接BC．

(1)、求点A、B、C的坐标．

(2)、点P为AB上的动点（点A、O、B除外），过点P作直线PN⊥x轴，交抛物线于点N，交直线BC于点M．设点P到原点的值为t，MN的长度为s，求s与t的函数关系式．

(3)、在（2）的条件下，试求出在点P运动的过程中，由点O、P、N围成的三角形与Rt△COB相似时点P的坐标．

查看试题解析