2012年广西河池市中考数学试卷
试卷更新日期：2017-05-12 类型：中考真卷
一、选择题.
-
1. 计算1﹣2的结果是（ ）A、﹣3 B、3 C、﹣1 D、12. 如图是由两个小正方体和一个圆锥体组成的立体图形，其主视图是（ ）
A、
B、
C、
D、
3. 下列事件是必然事件的是（ ）A、打开电视机，正在播放新闻联播 B、数据2，4，7，2，5的众数是7 C、某种彩票中奖率是1%，买这种彩票100张一定会中奖 D、两直线平行，同位角相等4. 如图，把一块含有45°角的直角三角板的两个顶点分别放在直尺的一组对边上．如果∠1=25°，那么∠2的度数是（ ）
A、30° B、25° C、20° D、15°5. 下列运算正确的是（ ）A、（﹣2a2）3=﹣8a6 B、a﹣2a=a C、a6÷a3=a2 D、（a+b）2=a2+b26. 如图，已知AB为⊙O的直径，∠CAB=30°，则∠D的度数为（ ）
A、30° B、45° C、60° D、80°7. 如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于E，垂足为D．若ED=5，则CE的长为（ ）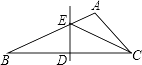
A、10 B、8 C、5 D、2.58. 下列图象中，表示y是x的函数的个数有（ ）
A、1个 B、2个 C、3个 D、4个9. 一元二次方程x2+2x+2=0的根的情况是（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、无实数根10. 用直尺和圆规作一个以线段AB为边的菱形，作图痕迹如图所示，能得到四边形ABCD是菱形的依据是（ ）
A、一组邻边相等的四边形是菱形 B、四边相等的四边形是菱形 C、对角线互相垂直的平行四边形是菱形 D、每条对角线平分一组对角的平行四边形是菱形11. 若a＞b＞0，则下列不等式不一定成立的是（ ）A、ac＞bc B、a+c＞b+c C、 D、ab＞b212. 如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN，连接CN．若△CDN的面积与△CMN的面积比为1：4，则 的值为（ ）
A、2 B、4 C、 D、二、填空题
-
13. 用激光测距仪测得两座山峰之间的距离为165000米，将数据165000用科学记数法表示为 ．14. 分解因式：x2﹣2x= ．15. 如图，AB、AC是⊙O的弦，OE⊥AB、OF⊥AC，垂足分别为E、F．如果EF=3.5，那么BC= ．
16. 有六张分别印有等边三角形、正方形、等腰梯形、正五边形、矩形、正六边形图案的卡片（这些卡片除图案不同外，其余均相同）．现将有图案的一面朝下任意摆放，从中任意抽取一张，抽到卡片的图案既是中心对称图形，又是轴对称图形的概率为 ．17. 从纸上剪下一个圆和一个扇形的纸片（如图），圆的半径为2，扇形的圆心角等于120°．若用它们恰好围成一个圆锥模型，则此扇形的半径为 ．
18.如图，在平面直角坐标系中，矩形OEFG的顶点F的坐标为（4，2），将矩形OEFG绕点O逆时针旋转，使点F落在y轴上，得到矩形OMNP，OM与GF相交于点A．若经过点A的反比例函数 的图象交EF于点B，则点B的坐标为 ．
三、解答题
-
19. 计算 ．20. 解分式方程： ．21. 如图，在10×10的正方形网格中，△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上．
(1)、填空：tanA= ， AC=（结果保留根号）；(2)、请你在图中找出一点D（仅一个点即可），连接DE、DF，使以D、E、F为顶点的三角形与△ABC全等，并加以证明．22. 某学校为了解学生课外阅读的情况，对学生“平均每天课外阅读的时间”进行了随机抽样调查，如图是根据调查结果绘制的两幅不完整的统计图．请你根据统计图提供的信息，解答以下问题：
(1)、平均每天课外阅读的时间为“0.5～1小时”部分的扇形图的圆心角为多少度；(2)、本次一共调查了多少名学生；(3)、将条形图补充完整；(4)、若该校有1680名学生，请估计该校有多少名学生平均每天课外阅读的时间在0.5小时以下．23. 手机上网已经成为当今年轻人时尚的网络生活，某网络公司看中了这种商机，推出了两种手机上网的计费方式：方式A以每分钟0.1元的价格按上网时间计费；方式B除收月基费20元外，再以每分钟0.06元的价格按上网时间计费．假设某客户月手机上网的时间为x分钟，上网费用为y元．
(1)、分别写出该客户按A、B两种方式的上网费y（元）与每月上网时间x（分钟）的函数关系式，并在右图的坐标系中画出这两个函数的图象；(2)、如何选择计费方式能使该客户上网费用更合算？24. 如图，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC于点E．
(1)、试判断DE与⊙O的位置关系，并证明你的结论；(2)、若∠C=30°，CE=6，求⊙O的半径．25. 随着人们环保意识的不断增强，我市家庭电动自行车的拥有量逐年增加．据统计，某小区2009年底拥有家庭电动自行车125辆，2011年底家庭电动自行车的拥有量达到180辆．(1)、若该小区2009年底到2012年底家庭电动自行车拥有量的年平均增长率相同，则该小区到2012年底电动自行车将达到多少辆？(2)、为了缓解停车矛盾，该小区决定投资3万元再建若干个停车位，据测算，建造费用分别为室内车位1000元/个，露天车位200元/个．考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，则该小区最多可建两种车位各多少个？试写出所有可能的方案．26.如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=﹣ x2+ x+4经过A、B两点．
(1)、写出点A、点B的坐标；(2)、若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；(3)、在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．