2012年广西贵港市中考数学试卷
试卷更新日期:2017-05-12 类型:中考真卷
一、选择题
-
1. ﹣2的倒数是( )A、﹣2 B、2 C、﹣ D、2. 计算(﹣2a)2﹣3a2的结果是( )A、﹣a2 B、a2 C、﹣5a2 D、5a23. 在一次投掷实心球训练中,小丽同学5次投掷的成绩(单位:cm)为:6,8,9,8,9,则关于这组数据的说法不正确的是( )A、极差是3 B、平均数是8 C、众数是8和9 D、中位数是94. 下列各点中在反比例函数y= 的图象上的是( )A、(﹣2,﹣3) B、(﹣3,2) C、(3,﹣2) D、(6,﹣1)5. 如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )A、正三角形 B、正四边形 C、正六边形 D、正八边形6.
如图是由若干个大小相同的正方体搭成的几何体的三视图,则该几何体所用的正方体的个数是( )
 A、2 B、3 C、4 D、57. 在平面直角坐标系中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )A、 B、 C、 D、8.
A、2 B、3 C、4 D、57. 在平面直角坐标系中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )A、 B、 C、 D、8.如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集在数轴上表示正确的是( )
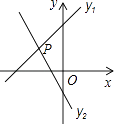 A、
A、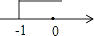 B、
B、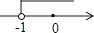 C、
C、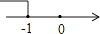 D、
D、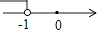 9. 从2,﹣1,﹣2三个数中任意选取一个作为直线y=kx+1中的k值,则所得的直线不经过第三象限的概率是( )A、 B、 C、 D、110.
9. 从2,﹣1,﹣2三个数中任意选取一个作为直线y=kx+1中的k值,则所得的直线不经过第三象限的概率是( )A、 B、 C、 D、110.如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是( )
 A、80° B、110° C、120° D、140°11.
A、80° B、110° C、120° D、140°11.如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )
 A、10 B、11 C、12 D、1312.
A、10 B、11 C、12 D、1312.如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABMD= AM2 .
其中正确结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 代数式 在实数范围内有意义,则x的取值范围是 .
14. 我国“神舟八号”飞船在太空上飞行约11000000千米,用科学记数法表示11000000为 .15.如图所示,直线a∥b,∠1=130°,∠2=70°,则∠3的度数是 .
 16.
16.如图,在△ABC中,∠A=50°,BC=6,以BC为直径的半圆O与AB、AC分别交于点D、E,则图中阴影部分面积之和等于(结果保留π).
 17.
17.如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 .
 18. 若直线y=m(m为常数)与函数y= 的图象恒有三个不同的交点,则常数m的取值范围是 .
18. 若直线y=m(m为常数)与函数y= 的图象恒有三个不同的交点,则常数m的取值范围是 .三、解答题
-
19.(1)、计算:|﹣ |+2﹣1+ (π﹣ )0﹣tan60°;(2)、解分式方程: .20.
如图,已知△ABC,且∠ACB=90°.
 (1)、请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
(1)、请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)、请判断直线BD与⊙A的位置关系(不必证明).21.如图,直线y= x与双曲线y= 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
 (1)、求A、B两点的坐标及双曲线的解析式;(2)、若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.22.
(1)、求A、B两点的坐标及双曲线的解析式;(2)、若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.22.某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段
频数
频率
60≤x<70
40
0.40
70≤x<80
35
b
80≤x<90
a
0.15
90≤x<100
10
0.10
频率分布统计表

请根据上述信息,解答下列问题:
(1)、分别求出a、b的值;(2)、请补全频数分布直方图;(3)、如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.23.如图,在▱ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.
 (1)、求证:AF=DF;(2)、若BC=2AB,DE=1,∠ABC=60°,求FG的长.24. 某公司决定利用仅有的349个甲种部件和295个乙种部件组装A、B两种型号的简易板房共50套捐赠给灾区.已知组装一套A型号简易板房需要甲种部件8个和乙种部件4个,组装一套B型号简易板房需要甲种部件5个和乙种部件9个.(1)、该公司组装A、B两种型号的简易板房时,共有多少种组装方案?(2)、若组装A、B两种型号的简易板房所需费用分别为每套200元和180元,问最少总组装费用是多少元?并写出总组装费用最少时的组装方案.25.
(1)、求证:AF=DF;(2)、若BC=2AB,DE=1,∠ABC=60°,求FG的长.24. 某公司决定利用仅有的349个甲种部件和295个乙种部件组装A、B两种型号的简易板房共50套捐赠给灾区.已知组装一套A型号简易板房需要甲种部件8个和乙种部件4个,组装一套B型号简易板房需要甲种部件5个和乙种部件9个.(1)、该公司组装A、B两种型号的简易板房时,共有多少种组装方案?(2)、若组装A、B两种型号的简易板房所需费用分别为每套200元和180元,问最少总组装费用是多少元?并写出总组装费用最少时的组装方案.25.如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
 (1)、直接写出线段AC、AD及⊙O半径的长;(2)、设PH=x,PC=y,求y关于x的函数关系式;(3)、当PH与⊙O相切时,求相应的y值.26.
(1)、直接写出线段AC、AD及⊙O半径的长;(2)、设PH=x,PC=y,求y关于x的函数关系式;(3)、当PH与⊙O相切时,求相应的y值.26.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,﹣1),交x轴于点A、B两点,交y轴于点C,其中点B的坐标为(3,0).
 (1)、求抛物线的解析式;(2)、设经过点C的直线与该抛物线的另一个点为D,且直线CD和直线CA关于直线CB对称,求直线CD的解析式;(3)、在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线OP与该抛物线交点的个数.
(1)、求抛物线的解析式;(2)、设经过点C的直线与该抛物线的另一个点为D,且直线CD和直线CA关于直线CB对称,求直线CD的解析式;(3)、在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线OP与该抛物线交点的个数.