浙江省温州市2019届高三数学2月高考适应性测试试卷

试卷更新日期：2019-04-22 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知i是虚数单位，则 $\frac{2 i}{1 + i}$ 等于（）

A、1 -I B、1 +I C、- 1 - I D、- 1＋i

查看试题解析
2. 已知集合 A＝{1，2，－1}，集合 B＝{y | y＝x² ， x∈A}，则A∪B＝（）

A、{1} B、{1，2，4} C、{-1，1，2，4} D、{1，4}

查看试题解析
3. 已知a，b都是实数，那么“ $3^{a} > 3^{b}$ ”是“ $a^{3} > b^{3}$ ” 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 双曲线 $2 y^{2} - x^{2} = 1$ 的一个顶点坐标是（）

A、( 2，0) B、( － $\frac{\sqrt{2}}{2}$ ，0) C、(0， $\sqrt{2}$ ) D、(0 ， $\frac{\sqrt{2}}{2}$ )

查看试题解析
5. 以下不等式组表示的平面区域是三角形的是（）

A、 ${\begin{matrix} x \geq 1 \\ x - y \geq 0 \\ x + 2 y - 6 \geq 0 \end{matrix}$ B、 ${\begin{matrix} x \geq 1 \\ x - y \geq 0 \\ x + 2 y - 6 \leq 0 \end{matrix}$ C、 ${\begin{matrix} x \geq 1 \\ x - y \leq 0 \\ x + 2 y - 6 \geq 0 \end{matrix}$ D、 ${\begin{matrix} x \geq 1 \\ x - y \leq 0 \\ x + 2 y - 6 \leq 0 \end{matrix}$

查看试题解析
6. 随机变量 X 的分布列如下表所示，

X

0

2

4

P

$\frac{1}{4}$

a

$\frac{1}{4}$

则 D X （）＝（）

A、1 B、2 C、3 D、4

查看试题解析
7. 在平面上， $\vec{e_{1}}$ ， $\vec{e_{2}}$ 是方向相反的单位向量，| $\vec{a}$ |＝2 ，( $\vec{b}$ - $\vec{e_{1}}$ ) •( $\vec{b}$ - $\vec{e_{2}}$ ) ＝0 ，则| $\vec{a}$ - $\vec{b}$ |的最大值为（）

A、1 B、2 C、4 D、3

查看试题解析
8. 已知实数 a> 0，b > 0，a≠1，且满足lnb ＝ $\frac{a - 1}{\sqrt{a}}$ ，则下列判断正确的是（）

A、a > b B、a <b C、 $l o g_{a}$ b > 1 D、 $l o g_{a}$ b <1

查看试题解析
9. 在正四面体 ABCD 中，P，Q分别是棱 AB，CD的中点，E，F分别是直线AB，CD上的动点，M 是EF 的中点，则能使点 M 的轨迹是圆的条件是（）

A、PE＋QF＝2 B、PE•QF＝2 C、PE＝2QF D、PE²＋QF²＝2

查看试题解析
10. 已知数列{ $x_{n}$ } 满足0<x₁< x₂ <π，且 $x_{n + 1} = {\begin{matrix} x_{n} + \sin x_{n} ， x_{n} \leq x_{n - 1} \\ x_{n} + \cos x_{n} ， x_{n} > x_{n - 1} \end{matrix} (n \geq 2)$ ，则（）

A、 $x_{3} < x_{4} ， x_{2019} < π$ B、 $x_{3} < x_{4} ， x_{2019} > π$ C、 $x_{3} > x_{4} ， x_{2019} < π$ D、 $x_{3} > x_{4} ， x_{2019} > π$

查看试题解析

二、填空题

11. 我国古代三国时期吴国的数学家赵爽创制了一幅如图所示的“勾股圆方图”，四个相同的直角三角形与边长为1的小正方形拼成一个边长为5的大正方形，若直角三角形的直角边分别记为a，b，有 ${\begin{matrix} a^{2} + b^{2} = 25 \\ \frac{1}{2} a b = 6 \end{matrix}$ ，则a＋b＝，其中直角三角形的较小的锐角的正切值为．

查看试题解析
12. 某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm³）等于，表面积（单位：cm²）等于．

查看试题解析
13. 若 $x^{6} = a_{0} + a_{1} (x + 1) + \dots + a_{5} {(x + 1)}^{5} + a_{6} {(x + 1)}^{6}$ ，则 $a_{0} + a_{1} + a_{2} + a_{3} + a_{4} + a_{5} + a_{6} =$ ， $a_{5} =$

查看试题解析
14. 在△ABC 中，C＝45°，AB＝6 ，D 为 BC 边上的点，且AD＝5，BD＝3 ，则cos B＝，AC＝．

查看试题解析
15. 已知某超市为顾客提供四种结账方式：现金、支付宝、微信、银联卡、若顾客甲只带了现金，顾客乙只用支付宝或微信付款，顾客丙、丁用哪种方式结账都可以，这四名顾客购物后，恰好用了其中的三种结账方式，那么他们结账方式的可能情况有种．

查看试题解析
16. 已知F是椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点，直线 $y = \frac{b}{a} x$ 交椭圆于A、B 两点，若cos∠AFB $= \frac{1}{3}$ ，则椭圆C 的离心率是．

查看试题解析
17. 已知 $f (x) = x^{2} - a x$ ，若对任意的 a∈R，存在 $x_{0}$ ∈[0，2] ，使得 $| f (x_{0}) | \geq k$ 成立，则实数k的最大值是

查看试题解析

三、解答题

18. 如图，在单位圆上，∠AOB＝a( $\frac{π}{6} < α < \frac{π}{2}$ )，∠ BOC＝ $\frac{π}{3}$ ，且△AOC的面积等于 $\frac{2 \sqrt{3}}{7}$ ．

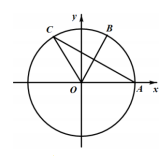
（I）求 sina 的值；

（II）求 2cos( $\frac{α}{2} - \frac{π}{3}$ )sin $\frac{α}{2} + \frac{π}{6}$ )

查看试题解析
19. 在三棱锥D-ABC中，AD⊥DC，AC⊥CB，AB＝2AD＝2DC＝2，且平面ABD⊥平面BCD，E为AC的中点．

（I）证明：AD⊥BC；

（II）求直线 DE 与平面ABD所成的角的正弦值．

查看试题解析
20. 设Sn为数列{an}的前n项和，且 S2＝8， $2 S_{n} = (n + 1) a_{n} + n - 1$ ．
（I）求a1，a2 并证明数列{an}为等差数列；

（II）若不等式 $λ \cdot 2^{n} - S_{n} > 0$ 对任意正整数 n 恒成立，求实数l的取值范围．

查看试题解析
21. 如图，A 为椭圆 $\frac{x^{2}}{2} + y^{2} = 1$ 的下顶点，过 A 的直线 l 交抛物线 $x^{2} = 2 p y (p > 0)$ 于B、C 两点，C 是 AB 的中点．

（I）求证：点C的纵坐标是定值；

（II）过点C作与直线 l 倾斜角互补的直线l'交椭圆于M、N两点，求p的值，使得△BMN的面积最大．

查看试题解析
22. 记 $f_{a} (x) = a x (x - 1) + ln x$
（I）若 $f_{a} (x) \leq 0$ 对任意的x>0恒成立，求实数a的值；

（II）若直线l： $y = k x + 1$ 与 $f_{a} (x)$ 的图像相切于点Q(m，n) ；

（i）试用m表示a与k；

（ii）若对给定的k，总存在三个不同的实数a1，a2，a3，使得直线l与曲线 $f_{a}_{1} (x)$ ， $f_{a_{2}} (x)$ ， $f_{a_{3}} (x)$ 同时相切，求实数k的取值范围。

查看试题解析

X	0	2	4
P	$\frac{1}{4}$	a	$\frac{1}{4}$