2012年广西北海市中考数学试卷

试卷更新日期：2017-05-11 类型：中考真卷

进入出卷网下载

一、选择题

1. 如果向东走5米记+5m，那么向西走3米记作（　　）

A、﹣2m B、﹣3m C、2m D、3m

查看试题解析
2.
如图，∠1的同位角是（　　）

A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
3. 在平面直角坐标系中将点P（2，﹣3）向上平移4个单位后得到点Q，则点Q的坐标是（　　）

A、（2，1） B、（2，﹣7） C、（6，﹣3） D、（﹣2，﹣3）

查看试题解析
4. 将数32507取近似值时，保留2个有效数字正确的是（　　）

A、32 B、33 C、33000 D、3.3×10⁴

查看试题解析
5. 下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A、等边三角形 B、平行四边形 C、正五边形 D、菱形

查看试题解析
6. 把多项式2x²﹣18分解因式，结果正确的是（　　）

A、2（x²﹣9） B、2（x+9）（x﹣9） C、2（x+3）（x﹣3） D、2（x﹣3）²

查看试题解析
7. 甲、乙两个兴趣小组参加了某次知识竞赛，辅导老师对两个小组竞赛成绩进行了统计，得到以下数据： $\bar{x_{甲}}$ =79， $\bar{x_{乙}}$ =82，S_甲²=82，S_乙²=79，则这两个小组成员的成绩比较稳定的是（　　）

A、甲组 B、乙组 C、两组一样 D、无法确定

查看试题解析
8.
如图，⊙O内切于△ABC，切点分别为D，E，F，连接OE，OF，DE，DF，乙组∠A=80°，则∠EDF等于（　　）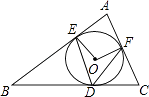

A、40° B、45° C、50° D、80°

查看试题解析
9. 下列计算正确的是（　　）

A、2m³+3m²=5m⁵ B、﹣5（﹣x³）^﹣²=﹣ $\frac{5}{x^{6}}$ C、（3a³b³）²=6a⁶b⁶ D、 $\sqrt{{(- 2)}^{2}}$ =﹣2

查看试题解析
10. 对于二次函数y=﹣2（x+4）²﹣3和它的图象，下列说法错误的是（　　）

A、抛物线开口向下 B、y随x的增大而减小 C、抛物线关于直线x=﹣4对称 D、抛物线不会经过第一象限

查看试题解析
11.
下面的三个图形是由若干个小正方形搭建而成的几何体的三视图，组成几何体的小正方形个数是（　　）

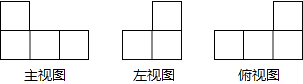A、7 B、6 C、5 D、4

查看试题解析
12. 已知△ABC中，AB=3，BC=4，AC的长是方程x²﹣12x+35=0的根，则△ABC的周长等于（　　）

A、12 B、14 C、12或14 D、以上都不是

查看试题解析

二、填空题

13. 化简：（25+4 $\sqrt{3}$ ）⁰﹣（﹣1）²⁰¹²+|﹣ $\sqrt{5}$ |= ．

查看试题解析
14. 当x时， $\sqrt{x + 1}$ 有意义．

查看试题解析
15.
如图，已知△ABC中BC=3cm，AC=4cm，AB=5cm，将△ABC绕AC旋转一周得到的几何体的侧面积为．

查看试题解析
16. 解方程 $\frac{2}{x - 3}$ = $\frac{3}{x}$ 得．

查看试题解析
17.
每年春季为预防流感，某校利用休息日对教室进行药熏消毒，已知药物燃烧过程及燃烧完后空气中的含药量y（mg/m³）与时间x（h）之间的关系如图所示，根据消毒要求，空气中的含药量不低于3mg/m³且持续时间不能低于10h．请你帮助计算一下，当空气中的含药量不低于3mg/m³时，持续时间可以达到h．

查看试题解析
18.
如图，在等腰三角形ABC中，∠BAC=90°，AB=AC=1，BD平方∠ABC，点P在BD上，⊙P切AB于点Q，则AP+PQ的最小值等于．

查看试题解析

三、解答题

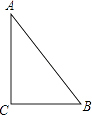
19. 解不等式2﹣x＞0，并把解集在数轴上表示出来．

查看试题解析
20.
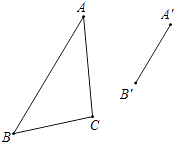
如图，已知△ABC和△A′B′C′是位似比为2的位似三角形，且AB的对应边是A′B′，请用尺规作图，将△A′B′C′补充完整（可不写作法，但保留作图痕迹）．

查看试题解析
21.
为了纪念中国共产主义青年团成立90周年，某校初三（1）、（2）班团支部组织了一次联欢会，小乐为活动设计了一个游戏：把两个可以自由转动的转盘各等分成三个扇形，分别标上1，2，3和4，5，6，每班级各派一名选手参加，每人同时转动两个转盘各一次（指针落在等分线上重转），转盘停止后，指针指向的数字之和为偶数时（1）班获胜，数字之和为奇数时（2）班获胜，小乐设计的游戏规则公平吗？请用树状图或列表分析说明，若认为不公平，请修改规则使游戏变得公平．

查看试题解析
22.
如图，在▱ABCD中，O为对角线AC的中点，EF经过点O并与AB，CD分别相交于点E，F．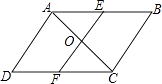

(1)、求证：AE=CF；

(2)、当EF⊥AC时，连接AF，CE，试判断四边形AFCE是怎样的四边形？并证明你的结论．

查看试题解析
23.
如图，为了测量合浦文昌塔的高度，某校兴趣小组在塔前的平地A处安装了测角仪，测得塔顶的仰角∠α=30°，又沿着塔的方向前进25米到达B处测量，测得塔顶的仰角∠β=45°，已知测角仪的高AC=1.5米，请你根据上述数据，计算塔FG的高度（结果精确到0.1米）．

查看试题解析
24. 某汽车出租公司为扩大业务，准备购置10辆客车，通过市场调查得到以下信息：
客车
座位
售价（万元）
每座日租金（元）
出租率
大型
40
45
80
55%
中型
25
35
80
70%

(1)、现公司预计用390万元购买两种客车，每种客车可以买多少辆？

(2)、如果公司可用的购车资金为380～400万元（含380万元和400万元），为使公司日收入最大，应如何确定购车方案？

查看试题解析
25.
如图，已知△ABP是等腰三角形，AB=BP，以AB为直径的⊙O交AP于点D，交BP于点C，连接BD交AC于点G，直线MN过点A，且∠PAM= $\frac{1}{2}$ ∠ABP．

(1)、试说明直线MN是⊙O的切线．

(2)、过D作DE⊥AB于E，交AC于F，求证：△DFG是等腰三角形．

(3)、连结FO，过点O作OQ⊥FO交BP于点Q，连结FQ，求证：FQ²=AF²+BQ² ．

查看试题解析
26.
如图，在平面直角坐标系中，直线y=﹣ $\frac{3}{4}$ x+3与坐标轴交于A，B两点，设P，Q分别为AB边，OB边上的动点，它们同时分别从点A，点O以每秒1个单位速度向终点B匀速移动，当一个点到达终点时另一个点也停止移动，设移动时间为t秒．

(1)、请写出点A，点B的坐标；

(2)、试求△OPQ的面积S与移动时间t之间的函数关系式，当t为何值时，S有最大值？并求出S的最大值；

(3)、试证明无论t为何值，△OPQ都不会是等边三角形；

(4)、将△OPQ沿直线PQ折叠，得到△O′PQ，问：△OPQ和O′PQ能否拼成一个三角形？若能，求出点O′的坐标；若不能，请说明理由．

查看试题解析

客车	座位	售价（万元）	每座日租金（元）	出租率
大型	40	45	80	55%
中型	25	35	80	70%