2012年广西百色市中考数学试卷
试卷更新日期:2017-05-11 类型:中考真卷
一、选择题
-
1. 计算:|﹣2012|=( )A、﹣2012 B、2012 C、 D、﹣2.
如图,已知l1∥l2 , ∠1=50°,则∠2的度数是( )
 A、50° B、100° C、120° D、130°3.
A、50° B、100° C、120° D、130°3.如图,这个几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 据中央新闻报道,我市因受强对流天气的影响,发生了严重的洪涝灾害.其中至5月25日止,凌云县就有7.6万人受灾.把数字76000用科学记数法表示为( )A、7.6×103 B、7.6×104 C、7.6×105 D、7.6×1065. 下列图形中,不是轴对称图形的是( )
4. 据中央新闻报道,我市因受强对流天气的影响,发生了严重的洪涝灾害.其中至5月25日止,凌云县就有7.6万人受灾.把数字76000用科学记数法表示为( )A、7.6×103 B、7.6×104 C、7.6×105 D、7.6×1065. 下列图形中,不是轴对称图形的是( )
A、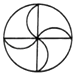 B、
B、 C、
C、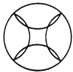 D、
D、 6. 下列各式计算正确的是( )A、﹣14=4 B、﹣2a+3b=﹣5ab C、﹣8ab÷(﹣2a)=﹣4 D、﹣2×3=﹣67. 计算:tan45°+( )﹣1﹣(π﹣ )0=( )A、2 B、0 C、1 D、﹣18. 不等式组 的解集在数轴上表示正确的是( )A、
6. 下列各式计算正确的是( )A、﹣14=4 B、﹣2a+3b=﹣5ab C、﹣8ab÷(﹣2a)=﹣4 D、﹣2×3=﹣67. 计算:tan45°+( )﹣1﹣(π﹣ )0=( )A、2 B、0 C、1 D、﹣18. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 9. 某校九年级(一)班学生在男子50米跑测试中,第一小组8名同学的测试成绩如下(单位:秒):7.0,7.2,7.5,7.0,7.4,7.5,7.0,7.8,则下列说法正确的是( )A、这组数据的中位数是7.4 B、这组数据的众数是7.5 C、这组数据的平均数是7.3 D、这组数据极差的是0.510.
9. 某校九年级(一)班学生在男子50米跑测试中,第一小组8名同学的测试成绩如下(单位:秒):7.0,7.2,7.5,7.0,7.4,7.5,7.0,7.8,则下列说法正确的是( )A、这组数据的中位数是7.4 B、这组数据的众数是7.5 C、这组数据的平均数是7.3 D、这组数据极差的是0.510.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
 A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC⊥BD时,四边形ABCD是菱形 D、当∠DAB=90°时,四边形ABCD是正方形11. 如图,CD是⊙O的直径,弦AB⊥CD于E,∠BCD=25°,则下列结论错误的是( )
A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC⊥BD时,四边形ABCD是菱形 D、当∠DAB=90°时,四边形ABCD是正方形11. 如图,CD是⊙O的直径,弦AB⊥CD于E,∠BCD=25°,则下列结论错误的是( ) A、AE=BE B、OE=DE C、∠AOD=50° D、D是 的中点12. 某县政府2011年投资0.5亿元用于保障性房建设,计划到2013年投资保障性房建设的资金为0.98亿元.如果从2011年到2013年投资此项目资金的年增长率相同,那么年增长率是( )A、30% B、40% C、50% D、60%13. 如图,在矩形ABCD中,AB=6cm,BC=4cm.动点E从点B出发,沿着线路BC→CD→DA运动,在BC段的平均速度是1cm/s,在CD段的平均速度是2cm/s,在DA段的平均速度是4cm/s,到点A停止.设△ABE的面积为y(cm2),则y与点E的运动时间t(s)的函数关系图象大致是( )
A、AE=BE B、OE=DE C、∠AOD=50° D、D是 的中点12. 某县政府2011年投资0.5亿元用于保障性房建设,计划到2013年投资保障性房建设的资金为0.98亿元.如果从2011年到2013年投资此项目资金的年增长率相同,那么年增长率是( )A、30% B、40% C、50% D、60%13. 如图,在矩形ABCD中,AB=6cm,BC=4cm.动点E从点B出发,沿着线路BC→CD→DA运动,在BC段的平均速度是1cm/s,在CD段的平均速度是2cm/s,在DA段的平均速度是4cm/s,到点A停止.设△ABE的面积为y(cm2),则y与点E的运动时间t(s)的函数关系图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 14. 如图,直线l1:x=1,l2:x=2,l3:x=3,l4:x=4,…,与函数y= (x>0)的图象分别交于点A1、A2、A3、A4、…;与函数y= 的图象分别交于点B1、B2、B3、B4、….如果四边形A1A2B2B1的面积记为S1 , 四边形A2A3B3B2的面积记为S2 , 四边形A3A4B4B3的面积记为S3 , …,以此类推.则S10的值是( )
14. 如图,直线l1:x=1,l2:x=2,l3:x=3,l4:x=4,…,与函数y= (x>0)的图象分别交于点A1、A2、A3、A4、…;与函数y= 的图象分别交于点B1、B2、B3、B4、….如果四边形A1A2B2B1的面积记为S1 , 四边形A2A3B3B2的面积记为S2 , 四边形A3A4B4B3的面积记为S3 , …,以此类推.则S10的值是( )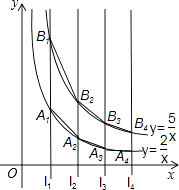 A、 B、 C、 D、
A、 B、 C、 D、二、填空题.
-
15. 若分式 的值为0,则x= .16.
如图,在Rt△ABC中,∠A=90°.小华用剪刀沿DE剪去∠A,得到一个四边形.则∠1+∠2=度.
 17. 一枚质地均匀的正方体,其六面分别刻有﹣2,0,﹣3,﹣2,5,4这六个数字.投掷这枚正方体一次,则向上一面的数字是﹣2的概率是 .18. 若规定一种运算为:a★b= (b﹣a),如3★5= (5﹣3)=2 .则 ★ = .19. 如图,Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转得到的,且A、O、B1三点共线.如果∠OAB=90°,∠AOB=30°,OA= .则图中阴影部分的面积为 . (结果保留π)
17. 一枚质地均匀的正方体,其六面分别刻有﹣2,0,﹣3,﹣2,5,4这六个数字.投掷这枚正方体一次,则向上一面的数字是﹣2的概率是 .18. 若规定一种运算为:a★b= (b﹣a),如3★5= (5﹣3)=2 .则 ★ = .19. 如图,Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转得到的,且A、O、B1三点共线.如果∠OAB=90°,∠AOB=30°,OA= .则图中阴影部分的面积为 . (结果保留π) 20. 如图,已知一动圆的圆心P在抛物线y= x2﹣3x+3上运动.若⊙P半径为1,点P的坐标为(m,n),当⊙P与x轴相交时,点P的横坐标m的取值范围是 .
20. 如图,已知一动圆的圆心P在抛物线y= x2﹣3x+3上运动.若⊙P半径为1,点P的坐标为(m,n),当⊙P与x轴相交时,点P的横坐标m的取值范围是 .
三、解答题
-
21. 先化简,再求值:( )÷ ,其中a= ﹣1.22. 我市某校为了了解九年级学生中考体育测试水平,从九年级随机抽取部分学生进行调查.把测试成绩分三个等级,A级:30分~24分,B级:23分~18分,C级:18分以下,并将调查结果绘制成如下图①、图②两个不完整的统计图.请根据图中信息解答下列问题:
 (1)、求出此次抽样调查学生人数和图②中C级所占扇形的圆心角的度数;(2)、将条形统计图补充完整;(3)、根据抽样调查结果,请你估计该校570名九年级学生中大约有多少名学生达标(包括A级和B级)23. 如图,在菱形ABCD中,E、F是对角线AC上的两点,且AE=CF.
(1)、求出此次抽样调查学生人数和图②中C级所占扇形的圆心角的度数;(2)、将条形统计图补充完整;(3)、根据抽样调查结果,请你估计该校570名九年级学生中大约有多少名学生达标(包括A级和B级)23. 如图,在菱形ABCD中,E、F是对角线AC上的两点,且AE=CF. (1)、图中有那几对全等三角形,请一一列举;(2)、求证:ED∥BF.24. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?25. 如图,在平面直角坐标系中,等腰梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上,且A(﹣4,0),B(6,0),D(0,3).
(1)、图中有那几对全等三角形,请一一列举;(2)、求证:ED∥BF.24. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?25. 如图,在平面直角坐标系中,等腰梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上,且A(﹣4,0),B(6,0),D(0,3). (1)、写出点C的坐标,并求出经过点C的反比例函数解析式和直线BC的解析式;(2)、若点E是BC的中点,请说明经过点C的反比例函数图象也经过点E.26. 如图,△ABC内接于⊙O,AB是直径,直线l是经过点C的切线,BD⊥l,垂足为D,且AC=8,sin∠ABC= .
(1)、写出点C的坐标,并求出经过点C的反比例函数解析式和直线BC的解析式;(2)、若点E是BC的中点,请说明经过点C的反比例函数图象也经过点E.26. 如图,△ABC内接于⊙O,AB是直径,直线l是经过点C的切线,BD⊥l,垂足为D,且AC=8,sin∠ABC= . (1)、求证:BC平分∠ABD;(2)、过点A作直线l的垂线,垂足为E(要求:用尺规作图,保留作图痕迹,不写作法、证明),并求出四边形ABDE的周长.27. 如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(﹣3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G.
(1)、求证:BC平分∠ABD;(2)、过点A作直线l的垂线,垂足为E(要求:用尺规作图,保留作图痕迹,不写作法、证明),并求出四边形ABDE的周长.27. 如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(﹣3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G. (1)、求抛物线的解析式;(2)、连接BE,求h为何值时,△BDE的面积最大;
(1)、求抛物线的解析式;(2)、连接BE,求h为何值时,△BDE的面积最大; (3)、已知一定点M(﹣2,0).问:是否存在这样的直线y=h,使△OMF是等腰三角形?若存在,请求出h的值和点G的坐标;若不存在,请说明理由.
(3)、已知一定点M(﹣2,0).问:是否存在这样的直线y=h,使△OMF是等腰三角形?若存在,请求出h的值和点G的坐标;若不存在,请说明理由.