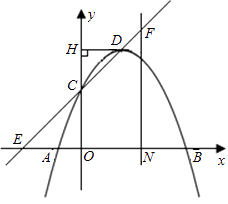2011年广西玉林市中考数学试卷
试卷更新日期:2017-05-11 类型:中考真卷
一、选择题
-
1. 计算2×(﹣1)的结果是( )A、﹣ B、﹣2 C、1 D、22. 若∠α的余角是30°,则cosα的值是( )A、 B、 C、 D、3. 下列运算正确的是( )A、2a﹣a=1 B、a+a=2a2 C、a•a=a2 D、(﹣a)2=﹣a24.
下列图形是轴对称图形,又是中心对称图形的有( )
 A、4个 B、3个 C、2个 D、1个5. 如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1=( )
A、4个 B、3个 C、2个 D、1个5. 如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1=( ) A、40° B、50° C、60° D、80°6. 已知二次函数y=ax2的图象开口向上,则直线y=ax﹣1经过的象限是( )A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限7.
A、40° B、50° C、60° D、80°6. 已知二次函数y=ax2的图象开口向上,则直线y=ax﹣1经过的象限是( )A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限7.如图,你能看出这个倒立的水杯的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 8.
8.如图,是我市5月份某一周的最高气温统计图,则这组数据(最高气温)的众数与中位数分别是( )
 A、28℃,29℃ B、28℃,29.5℃ C、28℃,30℃ D、29℃,29℃9. 已知拋物线y=﹣ x2+2,当1≤x≤5时,y的最大值是( )A、2 B、 C、 D、10. 小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
A、28℃,29℃ B、28℃,29.5℃ C、28℃,30℃ D、29℃,29℃9. 已知拋物线y=﹣ x2+2,当1≤x≤5时,y的最大值是( )A、2 B、 C、 D、10. 小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( ) A、2 B、 C、2 D、311. 如图,是反比例函数y= 和y= (k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=4,则k2﹣k1的值是( )
A、2 B、 C、2 D、311. 如图,是反比例函数y= 和y= (k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=4,则k2﹣k1的值是( ) A、1 B、2 C、4 D、812. 一个容器装有1升水,按照如下要求把水倒出:第1次倒出 升水,第2次倒出的水量是 升的 ,第3次倒出的水量是 升的 ,第4次倒出的水量是 升的 ,…按照这种倒水的方法,倒了10次后容器内剩余的水量是( )A、 升 B、 升 C、 升 D、 升
A、1 B、2 C、4 D、812. 一个容器装有1升水,按照如下要求把水倒出:第1次倒出 升水,第2次倒出的水量是 升的 ,第3次倒出的水量是 升的 ,第4次倒出的水量是 升的 ,…按照这种倒水的方法,倒了10次后容器内剩余的水量是( )A、 升 B、 升 C、 升 D、 升二、填空题
-
13. ﹣2011的相反数是 .14. 近似数0.618有个有效数字.
15. 分解因式:9a﹣a3= .16.如图,是某校三个年级学生人数分布扇形统计图,则九年级学生人数所占扇形的圆心角的度数为 .
 17. 如图,等边△ABC绕点B逆时针旋转30°时,点C转到C′的位置,且BC′与AC交于点D,则 的值为 .
17. 如图,等边△ABC绕点B逆时针旋转30°时,点C转到C′的位置,且BC′与AC交于点D,则 的值为 .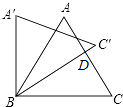 18. 如图,AB是半圆O的直径,以0A为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E.则下列四个结论:
18. 如图,AB是半圆O的直径,以0A为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E.则下列四个结论:①点D为AC的中点;②S△O′OE= S△AOC;③ ;④四边形O′DEO是菱形.其中正确的结论是 . (把所有正确的结论的序号都填上)

三、解答题.
-
19. 计算:( )﹣1﹣(5﹣π)0﹣|﹣3|+ .20. 已知:x1、x2是一元二次方程x2﹣4x+1的两个实数根.
求:(x1+x2)2÷( )的值.
21. 假日,小强在广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为10米,小强的身高AB为1.55米,请你帮小强画出测量示意图,并计算出风筝离地面的高度.(结果精确到1米,参考数据 ≈1.41, ≈1.73 ) 22. 如图,△OAB的底边经过⊙O上的点C,且OA=OB,CA=CB,⊙O与OA、OB分别交于D、E两点.
22. 如图,△OAB的底边经过⊙O上的点C,且OA=OB,CA=CB,⊙O与OA、OB分别交于D、E两点. (1)、求证:AB是⊙O的切线;(2)、若D为OA的中点,阴影部分的面积为 ,求⊙O的半径r.23. 一个不透明的纸盒中装有大小相同的黑、白两种颜色的围棋,其中白色棋子3个(分别用白A、白B、白C表示),若从中任意摸出一个棋子,是白色棋子的概率为 .(1)、求纸盒中黑色棋子的个数;(2)、第一次任意摸出一个棋子(不放回),第二次再摸出一个棋子,请用树状图或列表的方法,求两次摸到相同颜色棋子的概率.24. 上个月某超市购进了两批相同品种的水果,第一批用了2000元,第二批用了5500元,第二批购进水果的重量是第一批的2.5倍,且进价比第一批每千克多1元.(1)、求两批水果共购进了多少千克?(2)、在这两批水果总重量正常损耗10%,其余全部售完的情况下,如果这两批水果的售价相同,且总利润率不低于26%,那么售价至少定为每千克多少元?
(1)、求证:AB是⊙O的切线;(2)、若D为OA的中点,阴影部分的面积为 ,求⊙O的半径r.23. 一个不透明的纸盒中装有大小相同的黑、白两种颜色的围棋,其中白色棋子3个(分别用白A、白B、白C表示),若从中任意摸出一个棋子,是白色棋子的概率为 .(1)、求纸盒中黑色棋子的个数;(2)、第一次任意摸出一个棋子(不放回),第二次再摸出一个棋子,请用树状图或列表的方法,求两次摸到相同颜色棋子的概率.24. 上个月某超市购进了两批相同品种的水果,第一批用了2000元,第二批用了5500元,第二批购进水果的重量是第一批的2.5倍,且进价比第一批每千克多1元.(1)、求两批水果共购进了多少千克?(2)、在这两批水果总重量正常损耗10%,其余全部售完的情况下,如果这两批水果的售价相同,且总利润率不低于26%,那么售价至少定为每千克多少元?(利润率= )
25. 如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.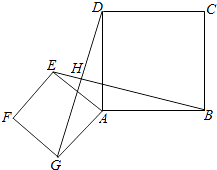 (1)、求证:EB=GD;(2)、判断EB与GD的位置关系,并说明理由;(3)、若AB=2,AG= ,求EB的长.26. 已知抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.(1)、求A、B的坐标;(2)、过点D作DH丄y轴于点H,若DH=HC,求a的值和直线CD的解析式;(3)、在第(2)小题的条件下,直线CD与x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求证:EB=GD;(2)、判断EB与GD的位置关系,并说明理由;(3)、若AB=2,AG= ,求EB的长.26. 已知抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.(1)、求A、B的坐标;(2)、过点D作DH丄y轴于点H,若DH=HC,求a的值和直线CD的解析式;(3)、在第(2)小题的条件下,直线CD与x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,则直线NF上是否存在点M,使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.